Exercise sheet 1: Nussinov algorithm
Exercise 1
Consider the RNA with the sequence:
S = GGGCACAUGGGGCAGUGCAGCCACUGAGCCand structure \(P\):
\(P = \{(1,30),(2,29),(4,17),(5,16),(6,15),(8,14),(9,13),(18,26),(19,25),(20,24)\}\)
1.1
Draw the structure \(P\) in dot-bracket notation and as a graphical representation.
Hide
Hint
If you note down the sequence along with the position numbers, it becomes easier to draft the dot-bracket notation. With this in hand, you can utilize the dot-bracket notation to sketch the structure. Assess the number of hairpins to gauge the amount of space required. Begin by illustrating one of the hairpins. In dot-bracket notation, a hairpin is represented as: ((…)).
Solution
1.2
Consider the structure \(P'=P\cup\{(11,22),(12,21)\}\) of sequence S.
Modify your drawings, where possible, in order to show the new structure \(P'\). Where does this fail and why?
Hide
Hint
Include the additional base pairs to the dot-bracket notation by using square brackets instead of round brackets, as before. Include an additional arc to the graph notation, on the corresponding position. If you’re unable to discern the problem this structure might cause, try sketching a linear Feynman diagram.
Solution
Problem: pseudoknot
The new base pairs/arcs \((11, 22)\) and \((12, 21)\) result in a pseudoknot. The bracket-only dot-bracket notation can not display pseudoknots. One would need to introduce a different symbol e.g. using square brackets [] to indicate the opening and closing positions of the crossing base pairs.
Exercise 2
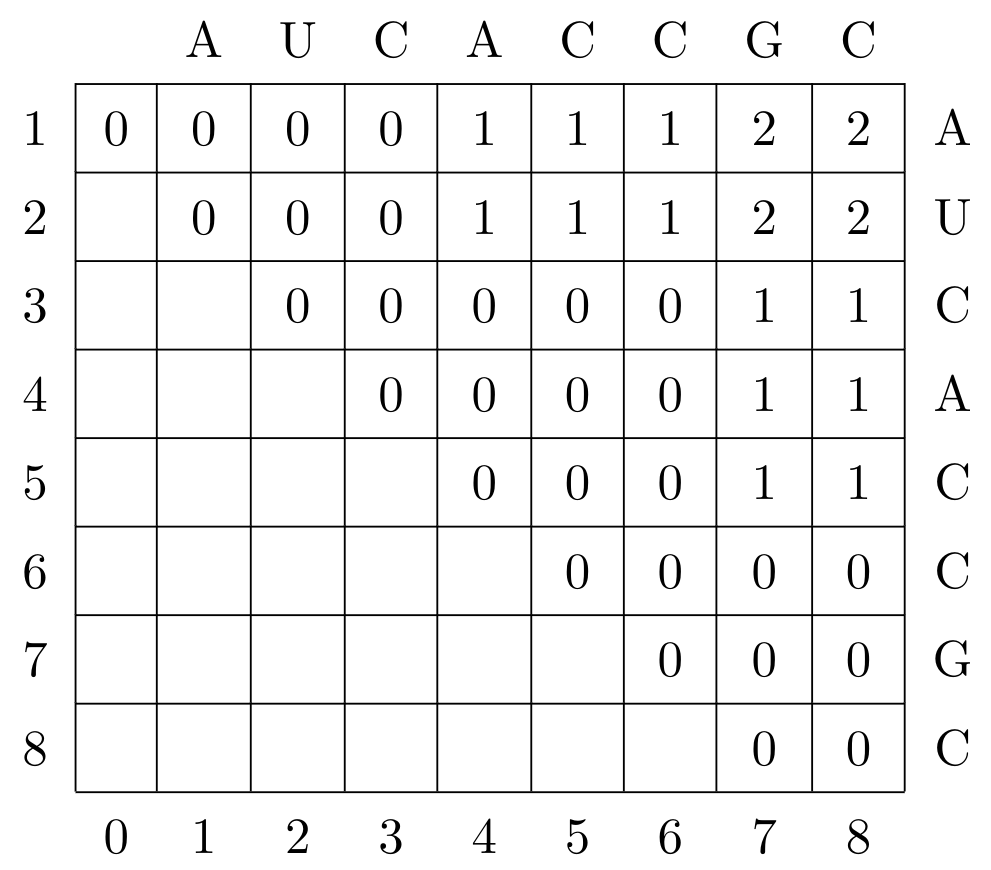
For a variation of the Nussinov algorithm with minimum loop length
\(1\), consider the following computed
Nussinov matrix \(N\) for the sequence
AUCACCGC:
2.1
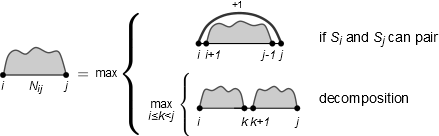
Compute the optimal structure according to the following recursion (considering loop length 1)!
Hide
Hint
Traceback starts in upper right corner: traceback(i,j). But you do not need to compute a traceback you can also find the structure just by looking at the sequence.
Solution
P = {(5,7),(2,4)}
2.2
Is there more than one optimal structure?
Hide
Hint 1
Considering a loop length of 1 means that at least one unpaired nucleotide must exist in a loop.
Solution
No, there is just one optimal structure \(P = \{(2,4),(5,7)\}\) when considering loop length 1.
Apart from the pairs \((5,7)\) and \((2,4)\), only positions \((2,7)\) and \((3,7)\) are possible, which only are present in structures that have just one base pair and are therefore not optimal.
2.3
Define all optimal tracebacks! Is there more than one optimal traceback?
Hide
Hint
There could be more than one optimal traceback for one optimal solution if the recursion is ambiguous.
Hint 2
Pseudo Code Traceback
Procedure traceback(i,j)
if (j <= i)
return
else if N_{i,j} = N_{i+1,j-1} +1, S_{i} and S_{j} complementary then
print(i,j)
traceback(i+1,j-1);
return
else
for all k: i <= k < j do
if N_{i,j} = N_{i,k} + N_{k+1,j} then
traceback(i,k); traceback(k+1,j)
return
end if
end for
end ifSolution
There are 5 possible tracebacks (for the same optimal structure):
- \(N_{1,8} \rightarrow N_{1,1}+N_{2,8}\)
- \(N_{1,1} \rightarrow \text{STOP}\)
- \(N_{2,8} \rightarrow N_{2,4}+N_{5,8}\)
- \(N_{2,4} \rightarrow N_{3,3}+bp (2,4)\)
- \(N_{3,3} \rightarrow \text{STOP}\)
- \(N_{5,8} \rightarrow N_{5,7}+N_{8,8}\)
- \(N_{5,7} \rightarrow N_{6,6}+bp (5,7)\)
- \(N_{6,6} \rightarrow \text{STOP}\)
- \(N_{8,8} \rightarrow \text{STOP}\)
- \(N_{1,8} \rightarrow N_{1,1}+N_{2,8}\)
- \(N_{1,1} \rightarrow \text{STOP}\)
- \(N_{2,8} \rightarrow N_{2,7}+N_{8,8}\)
- \(N_{2,7} \rightarrow N_{2,4}+N_{5,7}\)
- \(N_{2,4} \rightarrow N_{3,3}+bp (2,4)\)
- \(N_{3,3} \rightarrow \text{STOP}\)
- \(N_{5,7} \rightarrow N_{6,6}+bp (5,7)\)
- \(N_{6,6} \rightarrow \text{STOP}\)
- \(N_{8,8} \rightarrow \text{STOP}\)
- \(N_{1,8} \rightarrow N_{1,4}+N_{5,8}\)
- \(N_{1,4} \rightarrow N_{1,1}+N_{2,4}\)
- \(N_{1,1} \rightarrow \text{STOP}\)
- \(N_{2,4} \rightarrow N_{3,3}+bp (2,4)\)
- \(N_{3,3} \rightarrow \text{STOP}\)
- \(N_{5,8} \rightarrow N_{5,7}+N_{8,8}\)
- \(N_{5,7} \rightarrow N_{6,6}+bp (5,7)\)
- \(N_{6,6} \rightarrow \text{STOP}\)
- \(N_{8,8} \rightarrow \text{STOP}\)
- \(N_{1,8} \rightarrow N_{1,7}+N_{8,8}\)
- \(N_{1,7} \rightarrow N_{1,1}+N_{2,7}\)
- \(N_{1,1} \rightarrow \text{STOP}\)
- \(N_{2,7} \rightarrow N_{2,4}+N_{5,7}\)
- \(N_{2,4} \rightarrow N_{3,3}+bp (2,4)\)
- \(N_{3,3} \rightarrow \text{STOP}\)
- \(N_{5,7} \rightarrow N_{6,6}+bp (5,7)\)
- \(N_{6,6} \rightarrow \text{STOP}\)
- \(N_{8,8} \rightarrow \text{STOP}\)
- \(N_{1,8} \rightarrow N_{1,7}+N_{8,8}\)
- \(N_{1,7} \rightarrow N_{1,4}+N_{5,7}\)
- \(N_{1,4} \rightarrow N_{1,1}+N_{2,4}\)
- \(N_{1,1} \rightarrow \text{STOP}\)
- \(N_{2,4} \rightarrow N_{3,3}+bp (2,4)\)
- \(N_{3,3} \rightarrow \text{STOP}\)
- \(N_{5,7} \rightarrow N_{6,6}+bp (5,7)\)
- \(N_{6,6} \rightarrow \text{STOP}\)
- \(N_{8,8} \rightarrow \text{STOP}\)
2.4
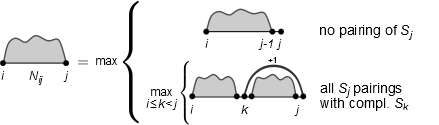
Does the last answer still hold for the following recursion (considering loop length 1)? Identify the possible traceback(s)!
Hide
Hint
What is different between these two recursions? How are the splits performed?
Solution
No, because the original Nussinov is not ambiguous.
Only if a base pair is found the sequence is separated into two parts for further recursion. In the first recursion, the sequence is always split unless there is a possible base pair. This generates several possible tracebacks for the same optimal sequence.
- \(N_{1,8} \rightarrow N_{1,7}\)
- \(N_{1,7} \rightarrow N_{1,4}+N_{6,6}+ bp(5,7)\)
- \(N_{1,4} \rightarrow N_{1,1}+N_{3,3}+ bp(2,4)\)
- \(N_{1,1} \rightarrow \text{STOP}\)
- \(N_{3,3} \rightarrow \text{STOP}\)
- \(N_{6,6} \rightarrow \text{STOP}\)
Exercise 3 (optional)
Implement the Nussinov algorithm as given in the lecture using a programming language of your choice.
Implement the computation of the Nussinov matrix:
Init: (for \(1\leq i\leq n\))
Recursion: (for \(1\leq i<j\leq n\)) \[ N_{ij} = \max \begin{cases} N_{ij-1}\\ \max_{\substack{i\leq k<j\\S_k, S_j complementary}} N_{ik-1} + N_{k+1j-1}\ +1\\ \end{cases} \]
Implement the traceback for the computation of an optimal structure. Print the resulting structure in dot-bracket notation.
Implement a modified traceback that counts the number of optimal structures.