Exercise 1 - entropy

Exercise 2 - partition function

Exercise 3 - Base pair and unpaired probabilities

Exercise 1 - entropy

We want to have a short look at the concept of entropy. Let $X$ be a discrete random variable with probabilities $p(i), (i=1,2,\ldots,n)$ . The amount of information to be associated with an outcome of probability $p(i)$ is defined as $I(p(i)) = \log_2(\frac{1}{p(i)})$ .

In information theory, the expected value of the information $I(X)$ for the random variable $X$ is called entropy. The entropy is given by

$H(X) = E[I(X)] = \sum_{i=1}^{n}p(i)\log_2(\frac{1}{p(i)}).$

Note that all logarithms in this exercise are base 2 (standard in information theory).

1.1

Compute the entropy of the probability distribution $p(1) = \frac{1}{2},\, p(2) = \frac{1}{4},\, p(3) = \frac{1}{8},\, p(4) = \frac{1}{8}$ .

Compute the expected value of the information of the random variable $E[I(X)]$ or entropy $H(X)$ as described above.

$\begin{align*} H(X) & = p(1)\log\left(\frac{1}{p(1)}\right) + p(2)\log\left(\frac{1}{p(2)}\right) + p(3)\log\left(\frac{1}{p(3)}\right) + p(4)\log\left(\frac{1}{p(4)}\right)\\ & = \frac{1}{2} + \frac{2}{4} + \frac{3}{8} + \frac{3}{8}\\ & = \frac{14}{8} \end{align*}$

1.2

Compute the entropy of the distribution $p(i) = \frac{1}{4},\: (i= 1,2,3,4)$ .

Hide
Solution

$\begin{align*} H(X) & = & 4 \cdot p(i) \log(\frac{1}{p(i)})\\ & = & 2 \end{align*}$

1.3

How can you explain the difference in entropy for both probability distributions?

Which of the two probability distributions has the higher information content, because you know more about an event before an event happened?

For the probability distribution in part 1. the information content of the probability distribution is higher than for 2. as we get more information from the distribution itself (e.g. we know that we are more likely to observe i=1).\ The information content for the event is higher for part 2. as we can learn more from the event (see coin example from the lecture).

This results in a higher entropy for the probability distribution in part 2..

Exercise 2 - partition function

Given the RNA sequence AUCACCGC and a minimal loop length of $1$ . Compute the partition function of the molecule using an energy function similar to the Nussinov algorithm: $E(P) = |P|$ that is the energy is the number of non-crossing base pairs of a given structure (only GC and AU pairs are to be considered).

Table of Boltzmann weights for $RT = 1$ :

2.1

Compute $Z$ via exhaustive structure space enumeration. (using the provided Boltzmann weights)

To compute Z you need to know all possible structures.

2.2

Compute the structure probability for each structure.

$Pr[P|S] = \frac{e^{(-\frac{E(P)}{RT})}}{\sum_{P'} e^{(-\frac{E(P)}{RT})}}$

2.3

Compare the structure probabilities in relation to each other. What is the structure probability of the open chain? What can you observe?

Hide
Solution

The open chain is more likely than any other structure including the optimal structure (here $P=\{(2,4)(5,7)\}$ ).

2.4

Is this result expected?

Base pairs usually stabilize a structure.

This is not expected, the open chain should not have a higher probability than the optimal structure.

2.5

If not how can you fix it? Test your idea by recalculating the structure probabilities!

How can you ensure that the open chain gets the lowest Boltzmann weight without changing the idea of scoring the number of base pairs for computing the energy of a structure?

The reason why the open chain has the highest probability is because the Bolzmann weight decreases with an increasing number of base pairs. The solution is to negate the energy function, i.e. $E(P) = -|P|$

We can now search for the optimal structure by energy minimization and the mfe structure is the most probable structure, as expected.

Exercise 3 - Base pair and unpaired probabilities

Given the corrected probabilities of the previous exercise for sequence AUCACCGC.

3.1

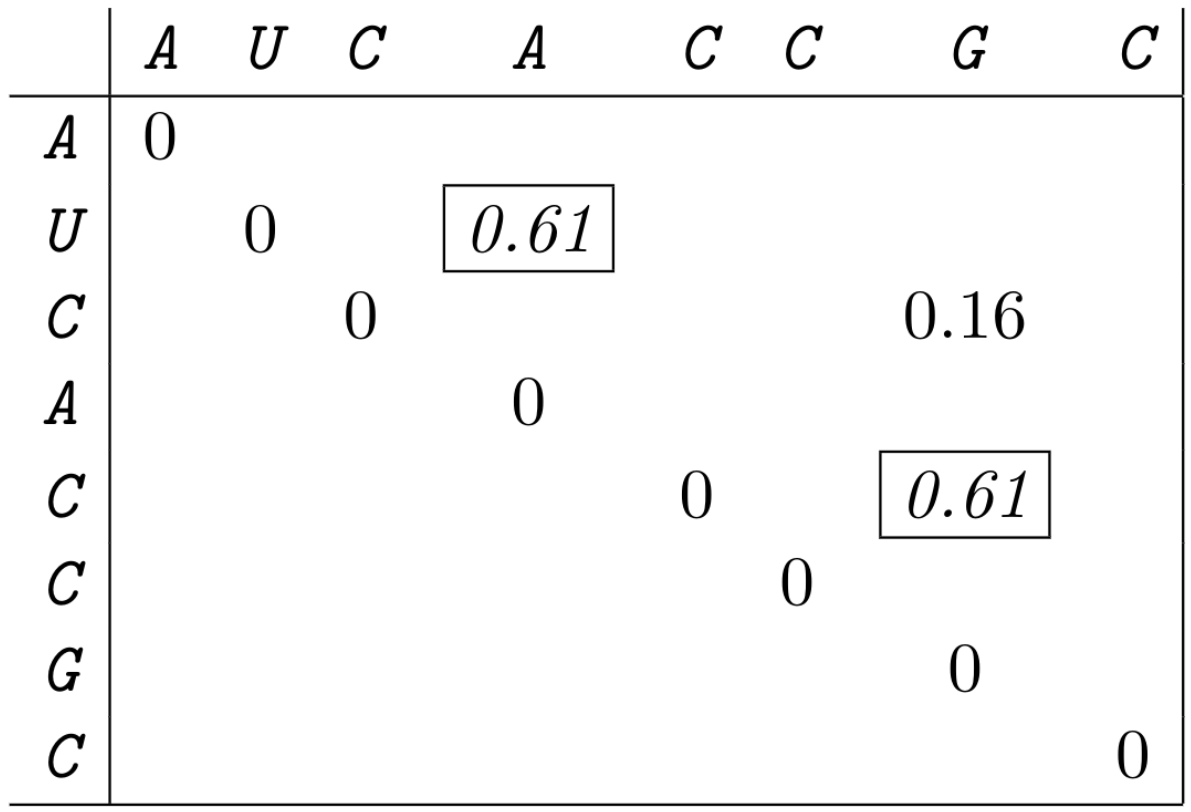
Compute and visualize the base pair probabilities in a dot-plot using your corrected energy function. (use the probability values instead of dots.)

Compute the base pair probabilities: $PR[(i,j)|S] = \sum_{P \ni (i,j)} Pr[P|S]$

3.2

Compute the probability $P^u(4)$ and $P^u(5)$ to be unpaired at sequence position 4 and 5, resp., and $P^u(4,5)$ that the subsequence $4..5$ is not involved in any base pairing.

$PR_{u}[(i,j)] = \frac{Z_{i,j}^u}{Z}$

$\begin{align*} P^u(4) &= 0.06 + 0.16 + 0.16 = 0.38\\ P^u(5) &= 0.06 + 0.16 + 0.16 = 0.38\\ P^u(4,5) &= 0.06 + 0.16 = 0.22 \end{align*}$

3.3

Why can’t we compute $P^u(4,5)$ from $P^u(4)$ and $P^u(5)$ using their product, i.e. why is $P^u(4,5) \neq P^u(4)\cdot P^u(5)$ ?

Are $P^u(4)$ and $P^u(5)$ independent?

The set of structures considered for $P^u(4,5)$ is a subset of both structure sets used to compute $P^u(4)$ and $P^u(5)$ . Thus, the two probabilities are not independent and can not be multiplied.

Exercise sheet 3: structure probability

Exercise 1 - entropy

1.1

1.2

1.3

Exercise 2 - partition function

2.1

2.2

2.3

2.4

2.5

Exercise 3 - Base pair and unpaired probabilities

3.1

3.2

3.3