Exercise sheet 6: Sankoff algorithm
Exercise 1
The Sankoff algorithm is obtained from the Zuker recursions by raising them from folding one sub-sequence to folding two sub-sequences. Furthermore, it adds the edit distance. Develop a simpler version of Sankoff that is obtained by starting the same construction from the simpler, but less efficient, form of the Zuker recursions
\[ C(i,j) = \min_{1 \leq k \leq 4} \left( \min_{s \text{ is a $k$-loop closed by } (i,j)} \left\{ e(s) + \sum_{(p,q) \text{ accessible in $s$ from } (i,j)} C(p,q) \right\} \right) \]
with the initial conditions \(C(i,i) = \infty\), and
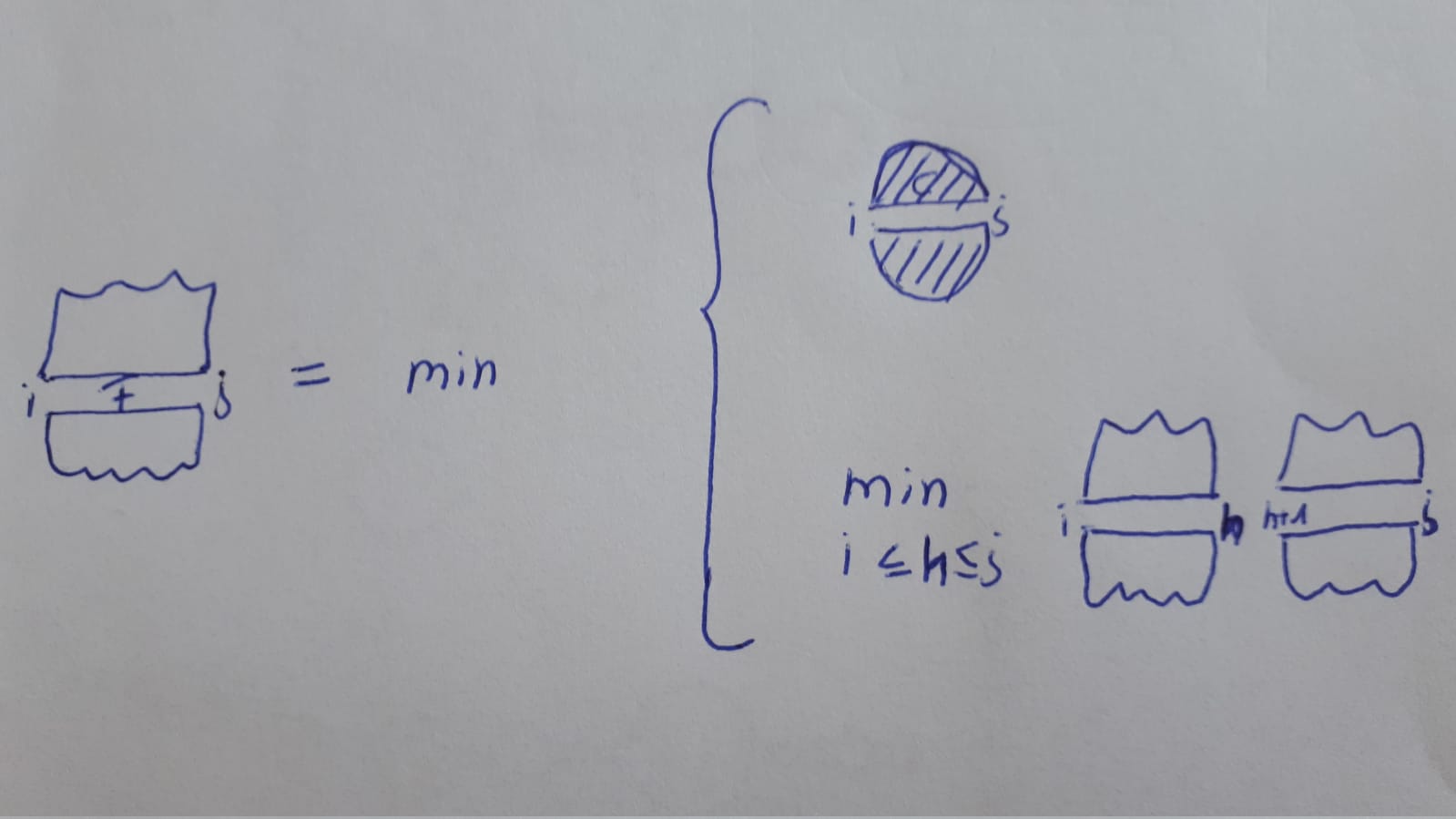
\[ F(i,j)= \min \begin{cases} C(i,j) , min_{i \leq h < j}\{ F(i,h) + F(h+1,j) \}\\ \end{cases} \]
with the initial conditions \(F(i,i) = 0\).
Furthermore, you can neglect the edit distance contribution. Make sure that your algorithm still has the same structural restrictions as the Sankoff algorithm, i.e. each hairpin is aligned to a hairpin, each multiloop is aligned to a corresponding multiloop and each 2-loop (including stackings and bulges) is aligned to at most one other 2-loop.
1.1
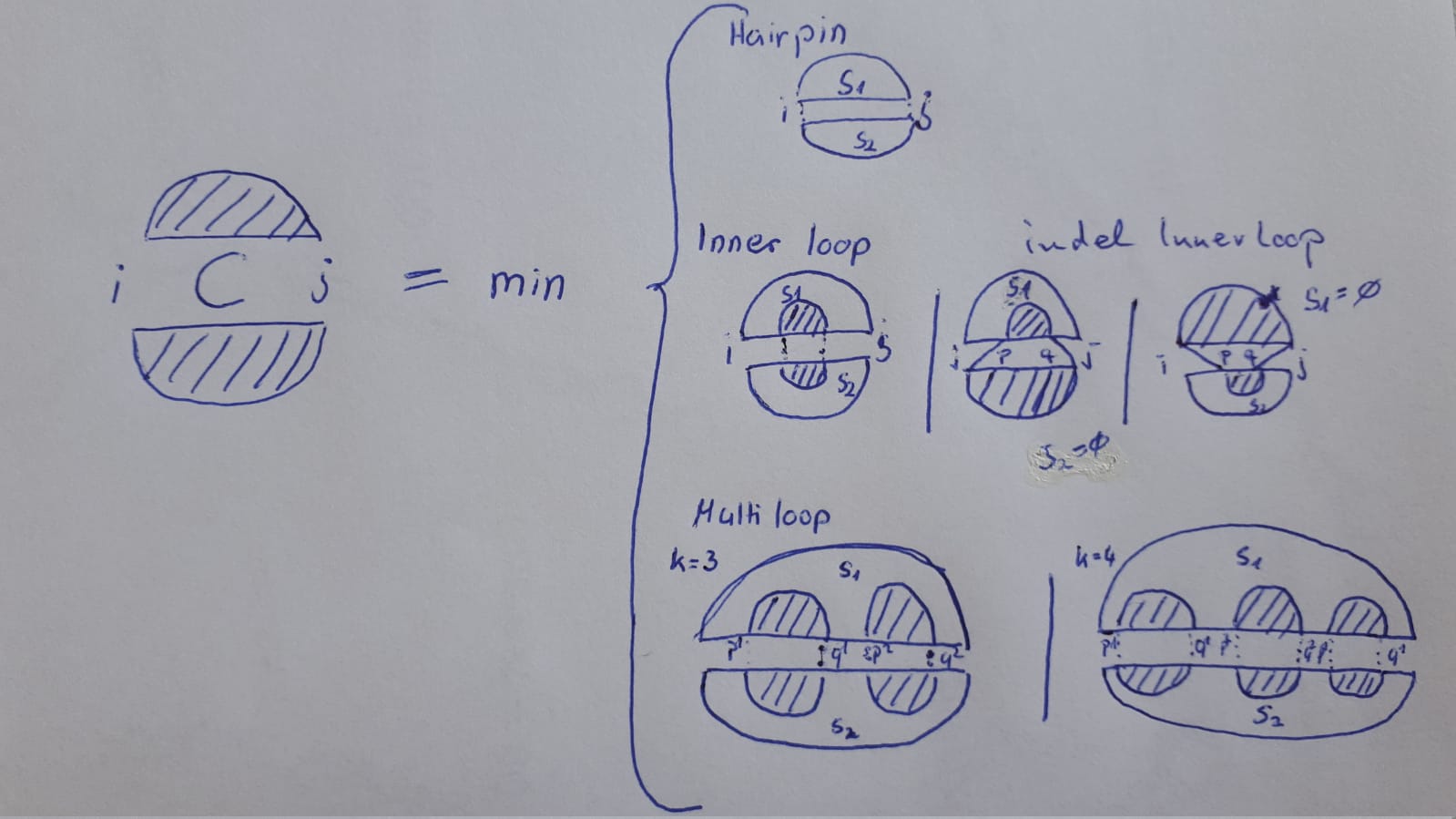
Generate respective recursion depictions for the translation of \(C\) and \(F\) into a Sankoff-style algorithm.
Hide
Solution
Decomposition into a hairpin and interior case analogously to the original Sankoff plus two explicit multi-loop cases for \(k=3\) and \(k=4\).
\[ C(i_{1},j_{1},i_{2},j_{2}) = \min \begin{cases} e(s_{1}) + e(s_{2}); & \text{where \(s_{1}, s_{2}\) are hairpin closing base pairs} (i_{1}, j_{1})(i_{2},j_{2}) \\ \min_{p_{1},q_{1},p_{2},q_{2}} \{e(s_{1}) + e(s_{2}) + C(p_{1},q_{1},p_{2},q_{2})\}; & \\ \min_{k > 2} \{e(s_{1}) + e(s_{2}) + \sum_{l=1}^{k-1} C(p_{1}^{l},q_{1}^{l},p_{2}^{l},q_{2}^{l})\} & \\ \end{cases} \]
\[ \text{where in the second case, \( s_{1}, s_{2} \) are 2-loops enclosed by \( i_{1},j_{1},i_{2},j_{2} \) with \( pq \) accessible.} \]
\[ F(i_{1},j_{1},i_{2},j_{2}) = \min \begin{cases} C(i_{1},j_{1};i_{2},j_{2})\\ min_{\substack{i_{1}\leq h_{1} \leq j_{1} \\ i_{2}\leq h_{2} \leq j_{2}}} \{F(i_{1},h_{1}; i_{2},h_{2}) + F(h_{1}+1, j_{1}; h_{2}+1, j_{2})\}\\ \end{cases} \]
1.2
What is the general complexity? What is the complexity without an upper bound for \(k\)?
Hide
Solution
here:
\(O(n^4)*O(n^{4*3}) = O(n^{16})\)
without upper bound on \(k\):
\(O(n^{4(k-1)+4})\) or \(O(n^{4*k})\)
1.3
What is the effect of omitting the edit distance contribution?
Hide
Solution
We only do simultaneous folding (mfe minimization) with helix alignment (since no sequence alignment contributions); no penalties for helix-length differences (since we do not score sequence similarity or indel gaps); Eventually, we find the best common structure shape, but sequence similarity of the respective alignment can be very bad (i.e. evolutionary unlikely).
1.4
Assume the derived recursion would incorporate sequence editing scores analogously to the original Sankoff approach via a respective matrix \(D\). What happens, if we apply very high gap scores within \(D\)?
Hide
Solution
Almost everything is aligned (matched or mismatched) and thus helix lengths should be very similar (interior loop indel less likely), ie overall it becomes a gap minimization problem and simultaneous folding becomes a ‘second level objective’.