Exercise 1

Please have a look at the reformulated recursion of the Jiang algorithm. In the lecture, some important properties have been omitted for sake of clarity. In this exercise your task is to explicitly state some of these properties.

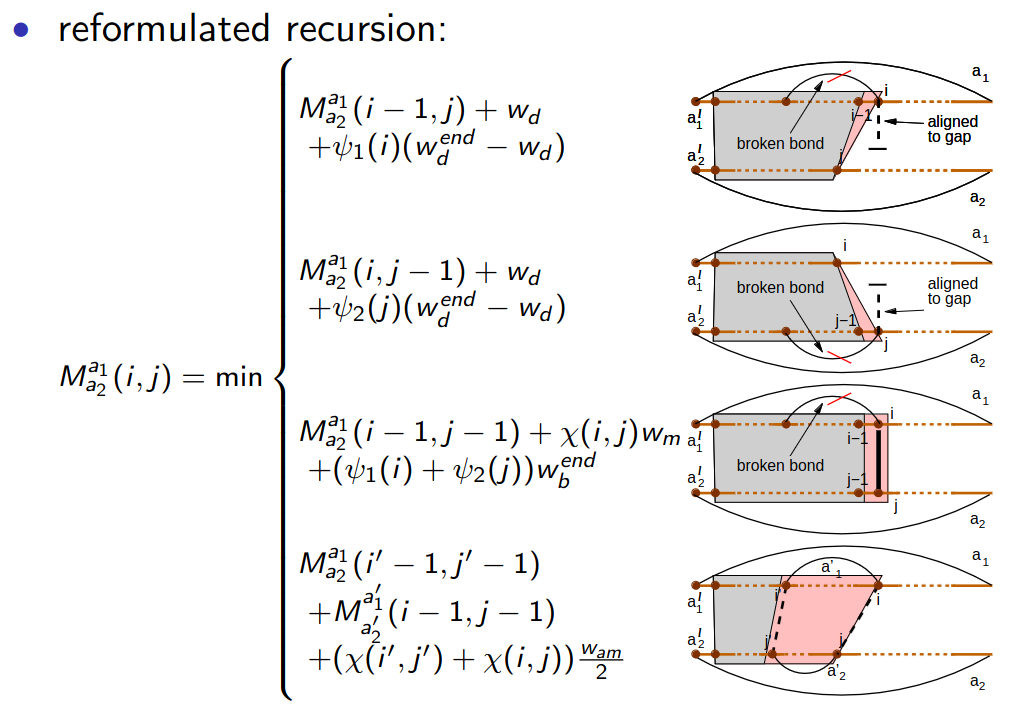
1.1

What are the base cases for the table entries, how should the tables be initialized?

Hide
Solution

The empty prefix of each M matrix has to be initialized with 0.

1.2

What value has to be assigned to entries outside of the tabulated M matrices, for example element \((3,4)\) in the first table of exercise 2?

Hide
Solution

The elements of the M matrices consist of prefix-alignment below 2 arcs. Any element outside these matrices is invalid and should never be used. Assign \(\infty\).

1.3

In what situation do we need to evaluate the fourth case of the recursion?

Hide
Solution

The fourth case has to be evaluated only if there exists a pair of arcs that lies completely inside of the evaluated arcs.

1.4

Which entry of each M matrix is used for the \(F\) matrix?

Hide
Solution

The matrix \(F\) stores the final values of all \(M\) matrices. The final values of the M-matrices are located at their lower right corners.

Exercise 2

We would like to align the following two structures with the reformulated recursion of the Jiang algorithm:

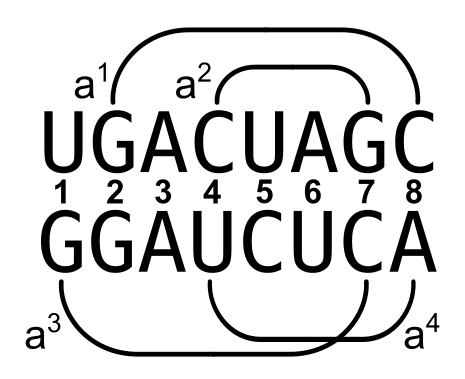
The cost for the different operations are \(w_d^{\text{end}}=2\), \(w_b^{\text{end}}=3\), \(w_{am}=6\), \(w_d=7\), and \(w_m=3\). The matrices \(M^{a_i,a_j}\) and \(F\) (with some missing entries) are given as follows:

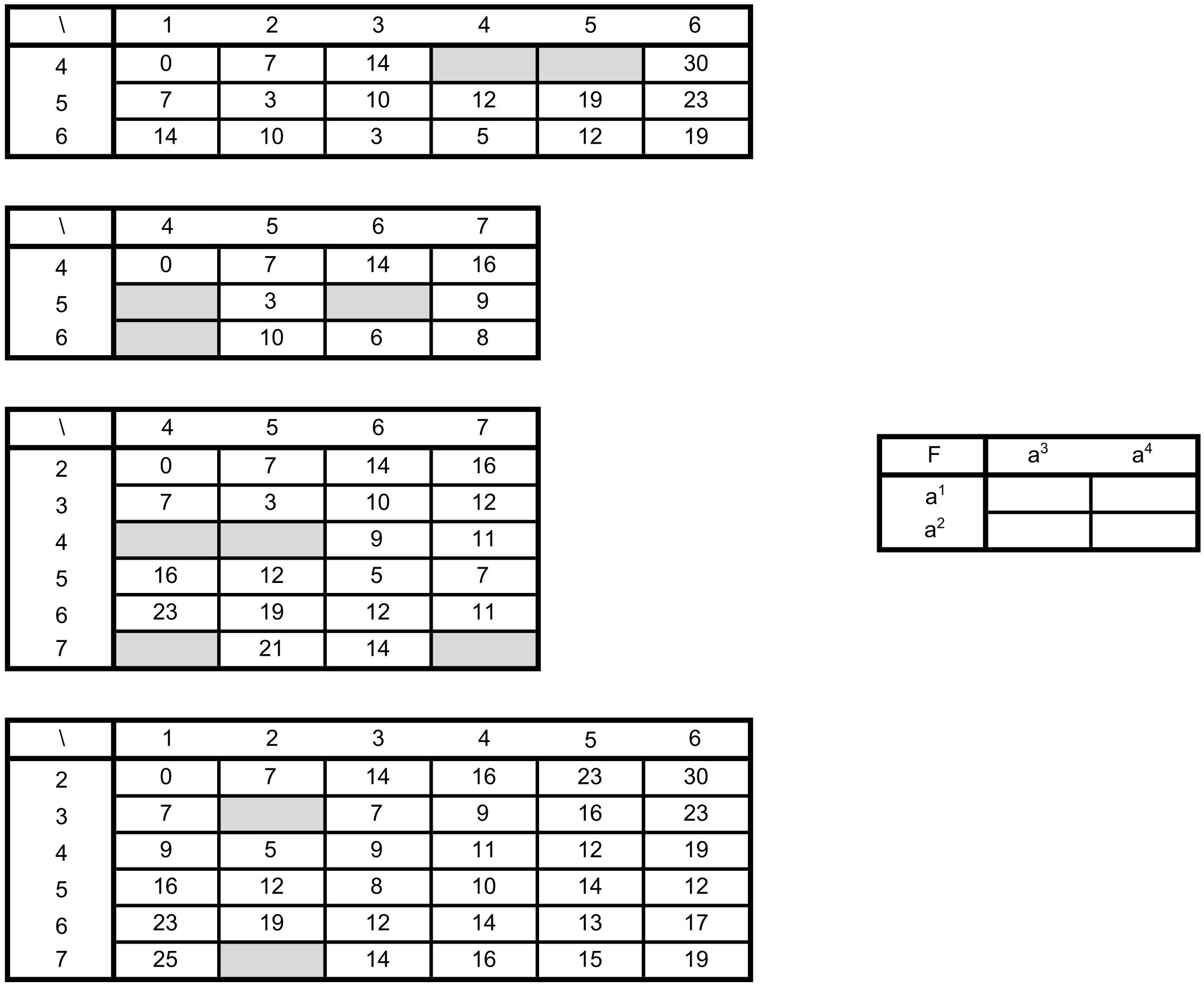
2.1

Which of the four matrices \(M^{a_i}_{a_j}\) on the left corresponds to which pair of arcs \(a_i\), \(a_j\)?

Hide
Solution
  1. \(M^{a_2,a_3}\)
  2. \(M^{a_2,a_4}\)
  3. \(M^{a_1,a_4}\)
  4. \(M^{a_1,a_3}\)

2.2

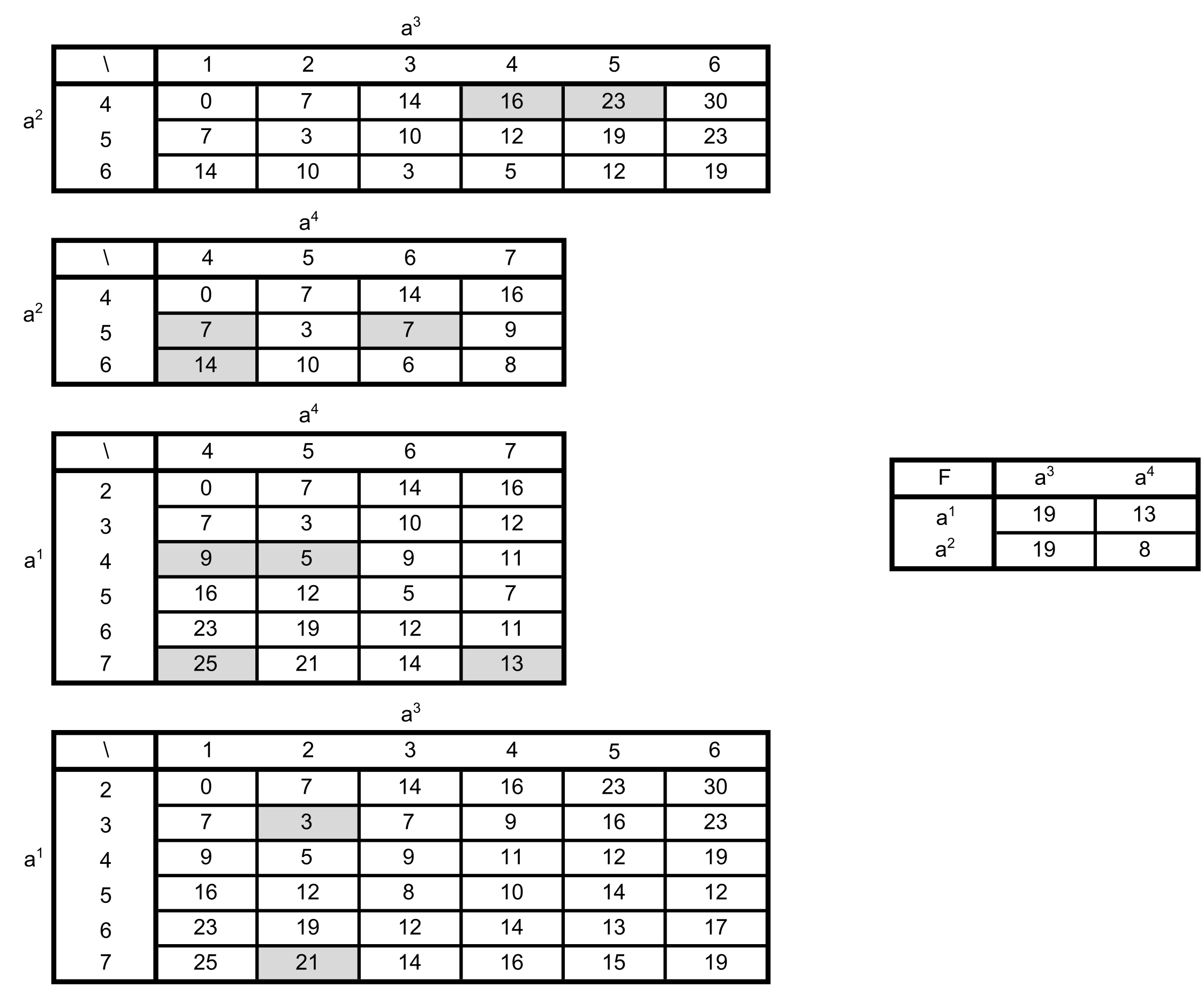
Calculate the missing values (shaded in grey) of the \(M^{a_i}_{a_j}\) matrices and also calculate the values of the \(F\)

Hide
Formula

Solution

Exercise 3

After having calculated the matrices \(M^{a_i}_{a_j}\) we compute the matrix containing the alignment of all prefixes of the entire sequences. Technically, this is a matrix \(M^{a_i}_{a_j}\) for some imaginary base pairs \(a_i=(0,9)\) and \(a_j=(0,9)\).

This matrix is given as:

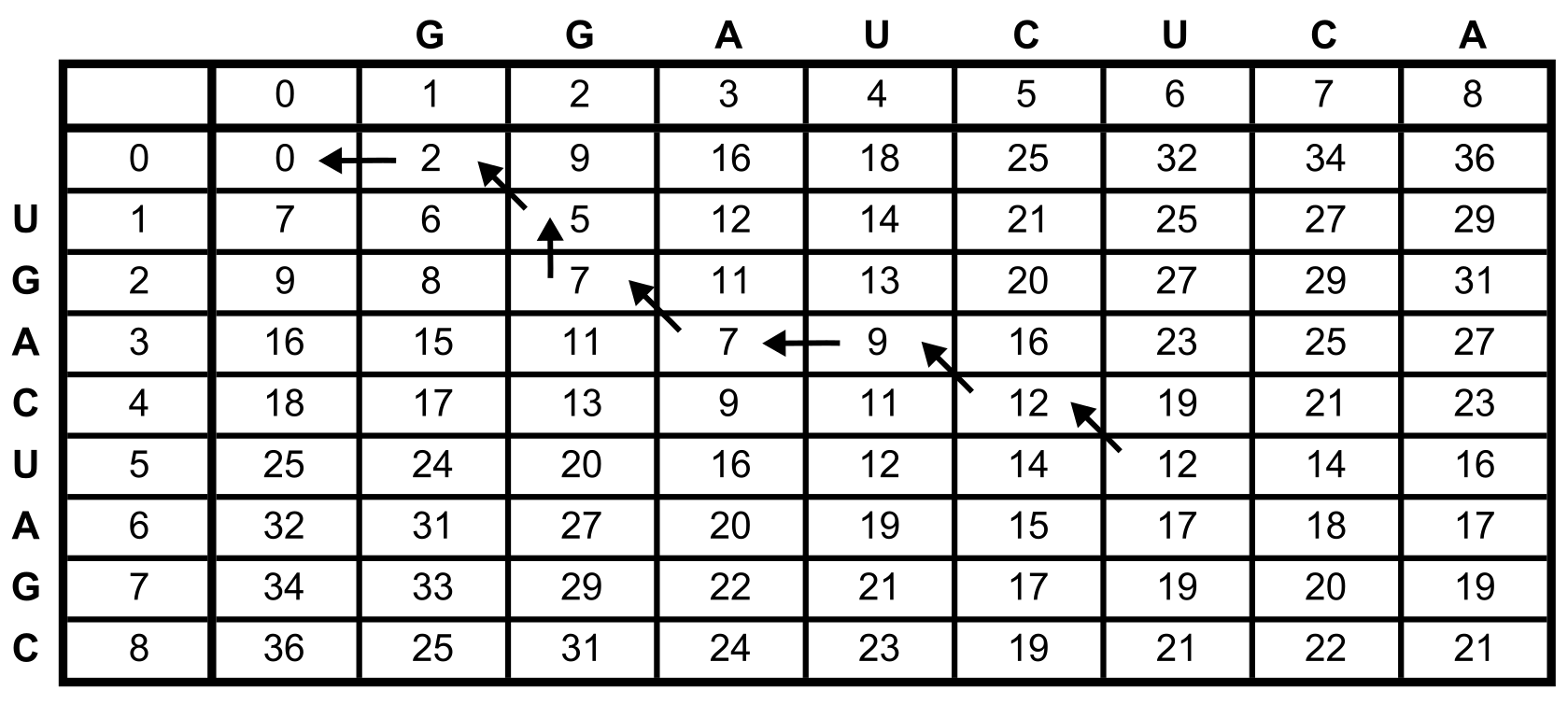
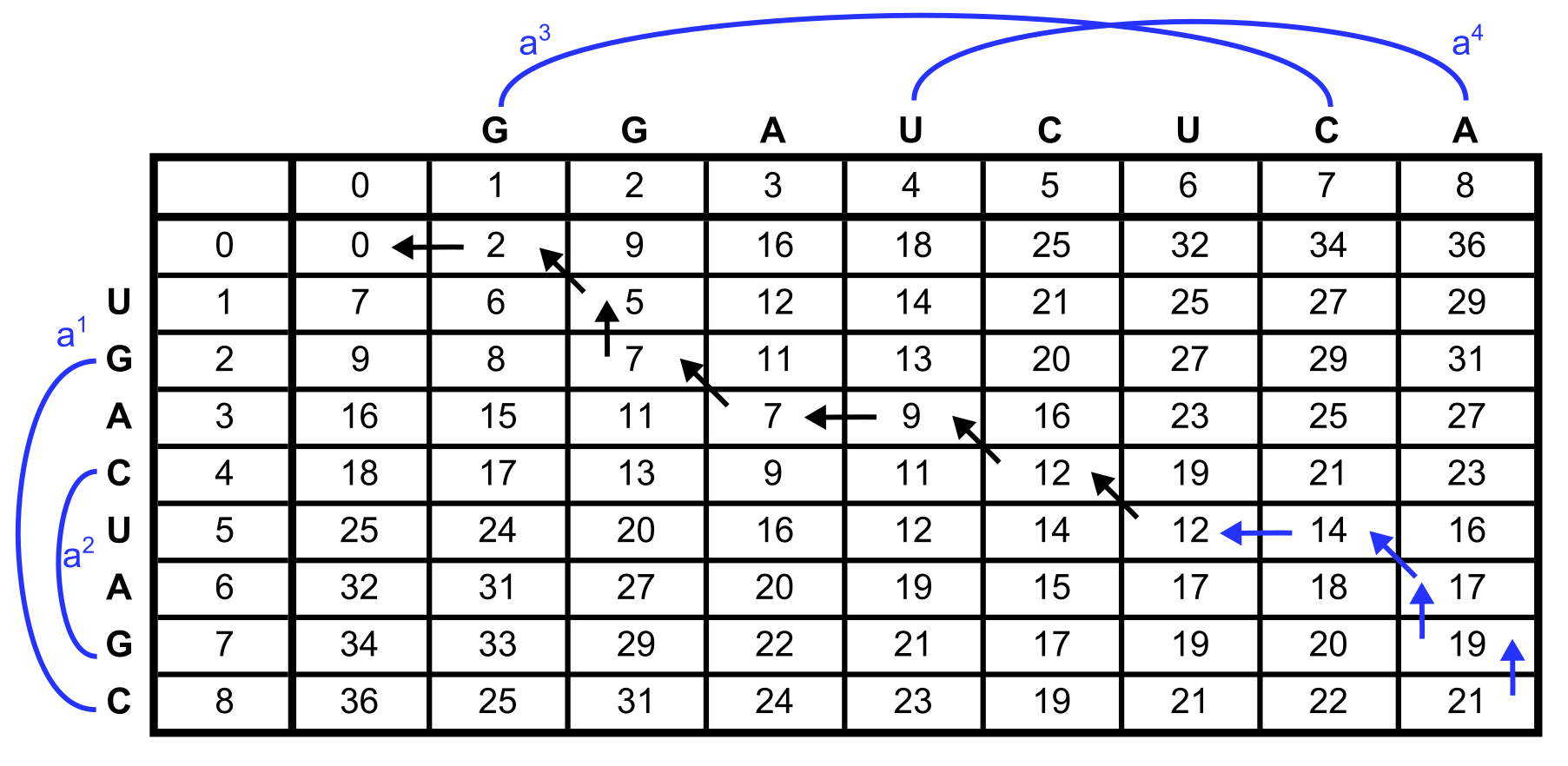
A part of the final backtrace is also already given by the arrows in the matrix. Give the missing part of the backtrace and also the alignment corresponding to the backtrace!

Hide
Solution

Traceback:

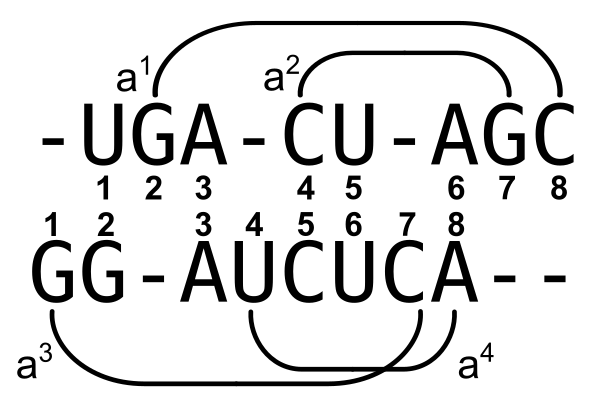
Alignment:

Example calculations for matrix M:

\[ M(0,1) = \min \left\{ \begin{array}{ll} + \infty, \\ M(0,0) + W_{d}^{\text{end}} & = 0 + 2 = \textbf{2}, \\ + \infty, \\ + \infty \end{array} \right. \]

\[ M(1,1) = \min \left\{ \begin{array}{ll} M(0,1) + W_d & = 2 + 7 = 9, \\ M(1,0) + W_{d}^{\text{end}} & = 7 + 2 = 9, \\ M(0,0) + W_m + W_{b}^{\text{end}} & = 0 + 3 + 3 = \textbf{6}, \\ + \infty \end{array} \right. \]

\[ M(7,7) = \min \left\{ \begin{array}{ll} M(6,7) + W_{d}^{\text{end}} & = 18 + 2 = \textbf{20}, \\ M(7,6) + W_{d}^{\text{end}} & = 19 + 2 = 21, \\ M(6,6) + W_m + 2 \cdot W_{b}^{\text{end}} & = 17 + 3 + 2 \cdot 3 = 26, \\ M(3,0) + M_{a_3}^{a_2}(6,6) + W_{am} & = 19 + 16 + 6 = 41 \end{array} \right. \]

Traceback calculations:

\[ M(8,8) = \min \left\{ \begin{array}{ll} M(7,8) + W_{d}^{\text{end}} & = 19 + 2 = \textbf{21}, \\ M(8,7) + W_{d}^{\text{end}} & = 22 + 2 = 24, \\ M(7,7) + W_m + 2W_{b}^{\text{end}} & = 20 + 3 + 6 = 29, \\ M(1,3) + M_{a_4}^{a_1}(7,7) + \frac{W_{am}}{2} & = 12 + 13 + 3 = 28 \end{array} \right. \]

\[ M(7,8) = \min \left\{ \begin{array}{ll} M(6,8) + W_{d}^{\text{end}} & = 17 + 2 = \textbf{19}, \\ M(7,7) + W_{d}^{\text{end}} & = 20 + 2 = 22, \\ M(6,7) + W_m + 2W_{b}^{\text{end}} & = 18 + 3 + 6 = 27, \\ + \infty \end{array} \right. \]

\[ M(6,8) = \min \left\{ \begin{array}{ll} M(5,8) + W_d & = 16 + 7 = 23, \\ M(6,7) + W_{d}^{\text{end}} & = 18 + 2 = 20, \\ M(5,7) + W_{b}^{\text{end}} & = 14 + 3 = \textbf{17}, \\ + \infty \end{array} \right. \]

\[ M(5,7) = \min \left\{ \begin{array}{ll} M(4,7) + W_d & = 21 + 7 = 28, \\ M(5,6) + W_{d}^{\text{end}} & = 12 + 2 = \textbf{14}, \\ M(4,6) + W_m + W_{b}^{\text{end}} & = 19 + 3 + 3 = 25, \\ + \infty \end{array} \right. \]