Exercise sheet 1: Hidden Markov models
Exercise 1 - Two kinds of dice

A casino uses two kinds of dice: \(98\%\) of dice are fair and \(2\%\) are loaded. The loaded die has a probability of \(0.5\) to show number six and \(0.1\) for the numbers one to five.
1a)
When we pick up a die from a table at random, what is the probability of rolling a six?
Hide
Hint 1 : Formulae
\[ L= \text{Loaded} \quad F= \text{Fair}\quad \mathcal{O}= \text{Observation}\\ P(\mathcal{O}) = P(F) \times P(\mathcal{O}|F) + P(L) \times P(\mathcal{O}|L) \]
Hint 2 : Calculation Method
\[ P(6) = 0.98 \times \frac{1}{6} + 0.02 \times \frac{1}{2} \]
Solution
\[ P(6) = 0.173\bar{3} \]
1b)
Hide
We pick up a die from a table at random and roll [⚅ ⚅ ⚅]. What is the probability, that the die is loaded.
Hint 1 : Formulae
\[ P(L|\mathcal{O}) = \frac{P(L,\mathcal{O})}{P(\mathcal{O})}\\ P(L,\mathcal{O}) = P(\mathcal{O}|L) \times P(L) \]
Hint 2 : Calculation Method
\[\begin{align*} P(L|\mathcal{O}) &= \frac{P(\mathcal{O}|L)\times P(L)}{P(\mathcal{O}|L)\times P(L) + P(\mathcal{O}|F)\times P(F)}\\ &= \frac{(\frac{1}{2})^3 \times 0.02}{(\frac{1}{2})^3 \times 0.02 + (\frac{1}{6})^3 \times 0.98} \end{align*}\]
Solution
\[ P(L|\mathcal{O}) = 35.53\% \]
1c)
How many sixes in a row would we need to roll to be at least 90% sure that the die is loaded?
Hide
Hint 1 : Formulae
\[ P(L|\mathcal{O}) = \frac{P(\mathcal{O}|L)\times P(L)}{P(\mathcal{O}|L)\times P(L) + P(\mathcal{O}|F)\times P(F)}\\ \]
Hint 2 : Calculation Method
\[\begin{alignat}{3} &P(L|\mathcal{O}) = \frac{\frac{2}{100}\times(\frac{1}{2})^n}{\frac{2}{100}\times(\frac{1}{2})^n + \frac{98}{100}\times(\frac{1}{6})^n} &&\geq 0.9 &&\quad| \text{ split } (\frac{1}{6})^n\\ &\iff \frac{\frac{2}{100}\times(\frac{1}{2})^n}{\frac{2}{100}\times(\frac{1}{2})^n + \frac{98}{100}\times(\frac{1}{2})^n \times (\frac{1}{3})^n} &&\geq \frac{9}{10} &&\quad| \text{ factorize}\\ &\iff \frac{\frac{2}{100}\times(\frac{1}{2})^n}{\frac{2}{100}\times(\frac{1}{2})^n \times (1 + 49 \times (\frac{1}{3})^n)} &&\geq \frac{9}{10} &&\quad| \text{ simplify, given } n > 0\\ &\iff \frac{1}{1 + 49 \times (\frac{1}{3})^n} &&\geq \frac{9}{10} &&\quad| \text{ cross-multiply, given } n > 0\\ &\iff \frac{9}{10} (1 + 49 \times (\frac{1}{3})^n) &&\leq 1 &&\quad| \text{ rewrite }\\ &\iff (\frac{1}{3})^n &&\leq \frac{1}{441} &&\quad| \text{ ln() }\\ &\iff n \times ln(\frac{1}{3}) &&\leq ln(\frac{1}{441}) &&\quad| \times\frac{1}{ln(\frac{1}{3})} \\ &\iff n &&\geq \frac{ln(\frac{1}{441})}{ln(\frac{1}{3})}\\ &\iff n &&\geq 5.542487... \end{alignat}\]
Solution
\[ n = 6 \text{, as only Integers make sense here (just trying would also work)} \]
Exercise 2 - The occasionally cheating casino

In a casino they use a fair die most of the time, but occasionally they switch to a loaded die. The loaded die has a probability \(0.5\) to show number six and probability \(0.1\) for the numbers one to five. Assume that the casino switches from a fair to a loaded die with probability \(0.05\) before each roll, and that the probability of switching back is \(0.1\). The probability to start a game with the fair die is \(0.9\).
2a)
Draw a graphical representation of the described Hidden Markov model.
Hide
Solution
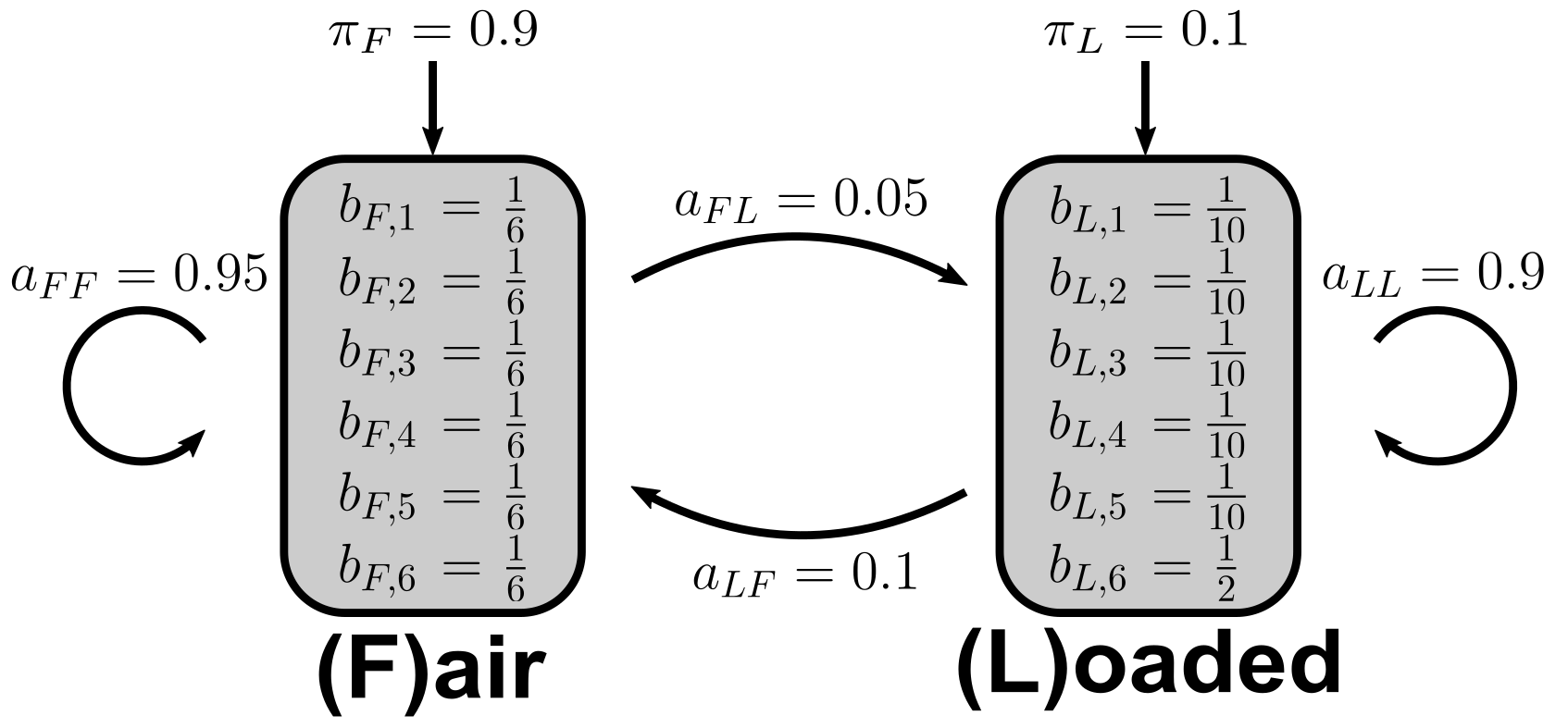
2b)
Given an observed sequence of outcomes \(\mathcal{O} = 3661634\) and two possible state sequences \(s_1 = LLLFFFF\) and \(s_2 = FFFFFFF\) (where \(F\) = Fair and \(L\) = Loaded), what are the joint probabilities \(P(\mathcal{O}, s_1)\) and \(P(\mathcal{O}, s_2)\) in the HMM described above?
Hide
Hint 1 : Formulae
\[ P(\mathcal{O}, s_x) = P(\mathcal{O}|s_x) \times P(s_x) \]
Hint 2 : Calculation Method
\[\begin{align*} P(s_1) =& \pi_L \times a_{LL}^2 \times a_{LF} \times a_{FF}^3 = 0.1 \times 0.9^2 \times 0.1 \times (0.95)^3 = 0.0069 \\ P(s_2) =& \pi_F \times a_{FF}^6 = 0.9 \times 0.95^6 = 0.6616 \\ P(\mathcal{O}|s_1) =& b_{L,3} \times b_{L,6}^2 \times b_{F,1} \times b_{F,6} \times b_{F,3} \times b_{F,4} = 0.1 \times 0.5^2 \times (\frac{1}{6})^4 = 1.9 \times 10^{-5} \\ P(\mathcal{O}|s_2) =& b_{F,3} \times b_{F,6}^2 \times b_{F,1} \times b_{F,6} \times b_{F,3} \times b_{F,4} = (\frac{1}{6})^7 = 3.57 \times 10^{-6} \\ P(\mathcal{O},s_1) =& P(\mathcal{O}|s_1) \times P(s_1)= 1.9 \times 10^{-5} \times 0.0069 \\ P(\mathcal{O},s_2) =& P(\mathcal{O}|s_2) \times P(s_2)= 3.57 \times 10^{-6} \times 0.6616 \end{align*}\]
Solution
\[\begin{align*} P(\mathcal{O},s_1) &= 1.34 \times 10^{-7}\\ P(\mathcal{O},s_2) &= 2.36 \times 10^{-6} \end{align*}\]
2c)
Give an observation \(\mathcal{O} = 1662\), how many possible state sequences exist in the described HMM?
Hide
Hint 1
The actual observation does not matter in this case because all emission probabilities are \(>0\). There are \(2^4\) possible state sequences.
Solution
There are \(16\) possible state sequences.
Exercise 3 - Programming assignment
For the programming tasks, please follow the instructions given in GitHub Classroom under the following links.