Exercise 1

You are given the text T=CAGTAGTAGC.

1a)

Draw the corresponding suffix tree!

Hide
Solution

1b)

Describe the steps of a counting query for \(P =\) TAG.

Hide
Solution
  • start at root node
  • locate outgoing edge that starts with \(T\)
  • match subsequent characters of the pattern
  • in the subtree rooted at TAG count the number of leaves \(\Rightarrow 2\)

1c)

Describe the steps of a reporting query for \(P =\) AG.

Hide
Solution
  • start at root node
  • locate outgoing edge that start with \(A\)
  • match subsequent characters of the pattern
  • in the subtree rooted at AG report the labels of all leaves \(\Rightarrow \{2, 5, 8\}\)

Exercise 2

2a)

Draw a generalized suffix tree for the sequences \(A=\)CCATG and \(B=\) CATG.

Hide
Hint 1

Concatenate the two sequences using a unique character for splitting. e.g. CCATG#CATG$.

Dont forget to include suffix links!

Formulae

\(sl(v) = w\)

\(\overline{v} = cb\)

\(\overline{w} = b\)

\(c: character, b: string\)

remember: \(\overline{v}\) denotes the concatenation of all path labels from the root to v.

Solution

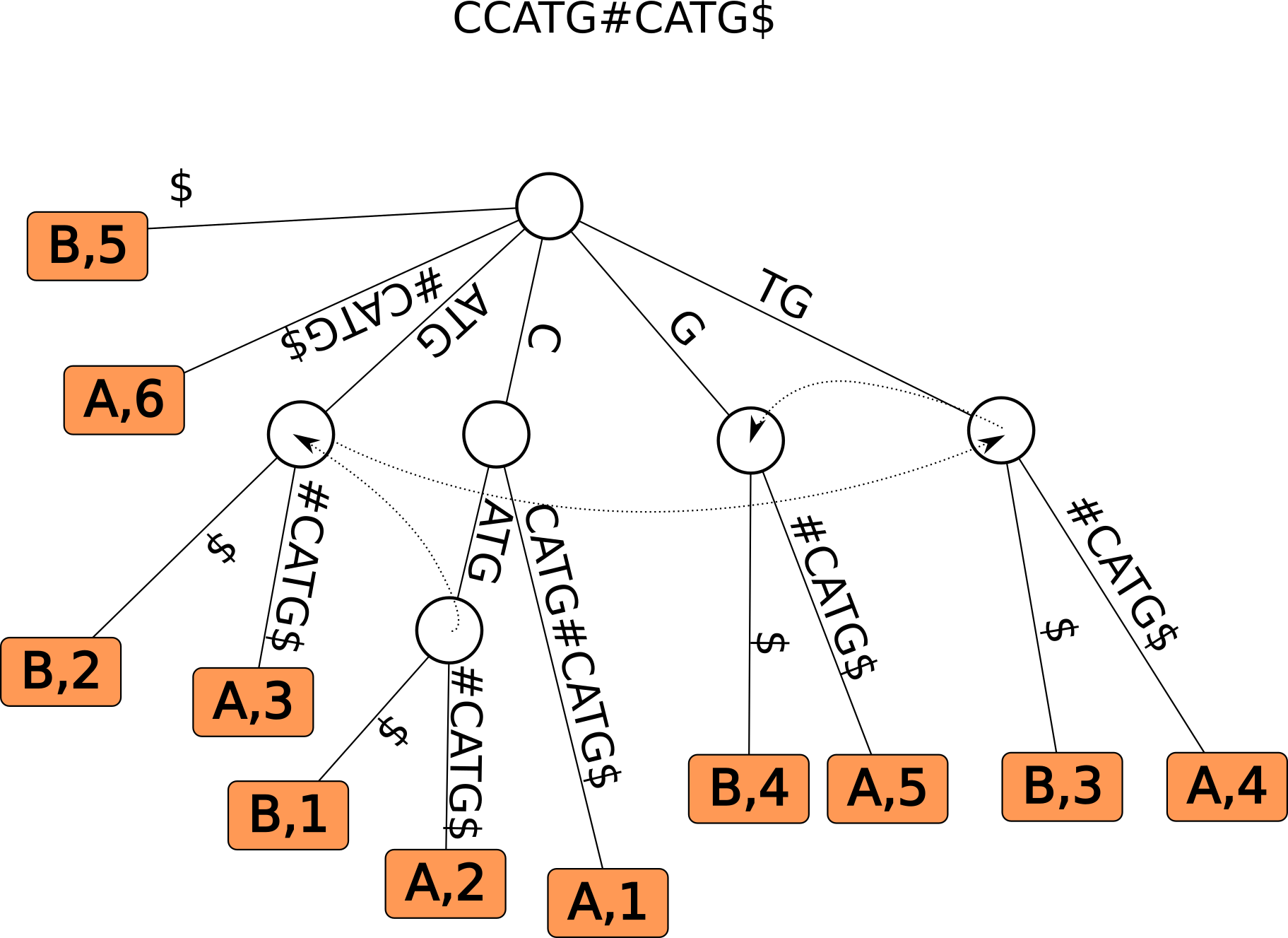
2b)

Find the Maximal Unique Matches of the sequences \(A=\)CCATG and \(B=\)CATG using the tree from A).

Hide
Solution

CATG is the only MUM as \(\overline{v} =\) CATG has no suffix links pointing to it

Exercise 3

3a)

Draw a generalized suffix tree for the sequence \(A=\)ACGCACGCG.

Hide
Solution

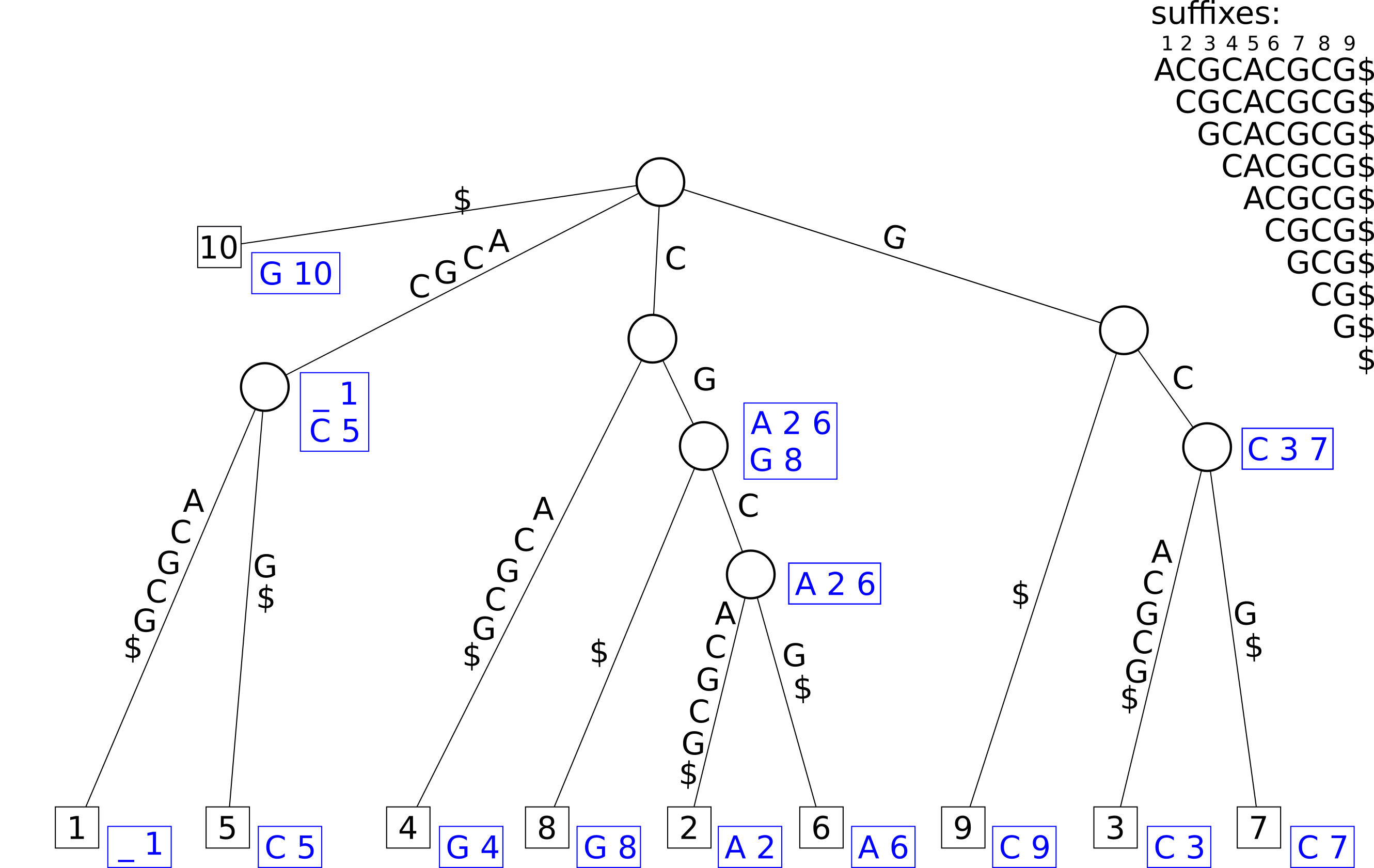
3b)

Find all maximal pairs of length at least 2.

Hide
Solution

ACGC: \((1,5,4)\)

CG: \((2,8,2), (6,8,2)\)

3c)

Why is C: \((2, 8, 1)\) not a maximal pair?

Hide
Solution

It is not right maximal. This can be seen since CG: \((2, 8, 2)\) already includes the indices 2 and 8 with a longer match.