Exercise sheet 5: Probalign
For the following exercises on Probalign, we use an affine gap penalty with \(g(k) = \alpha + \beta k = -0.5 - 0.25k\), there temperature \(T=1\) and the similarity function \(\sigma(x_i, y_j)\):
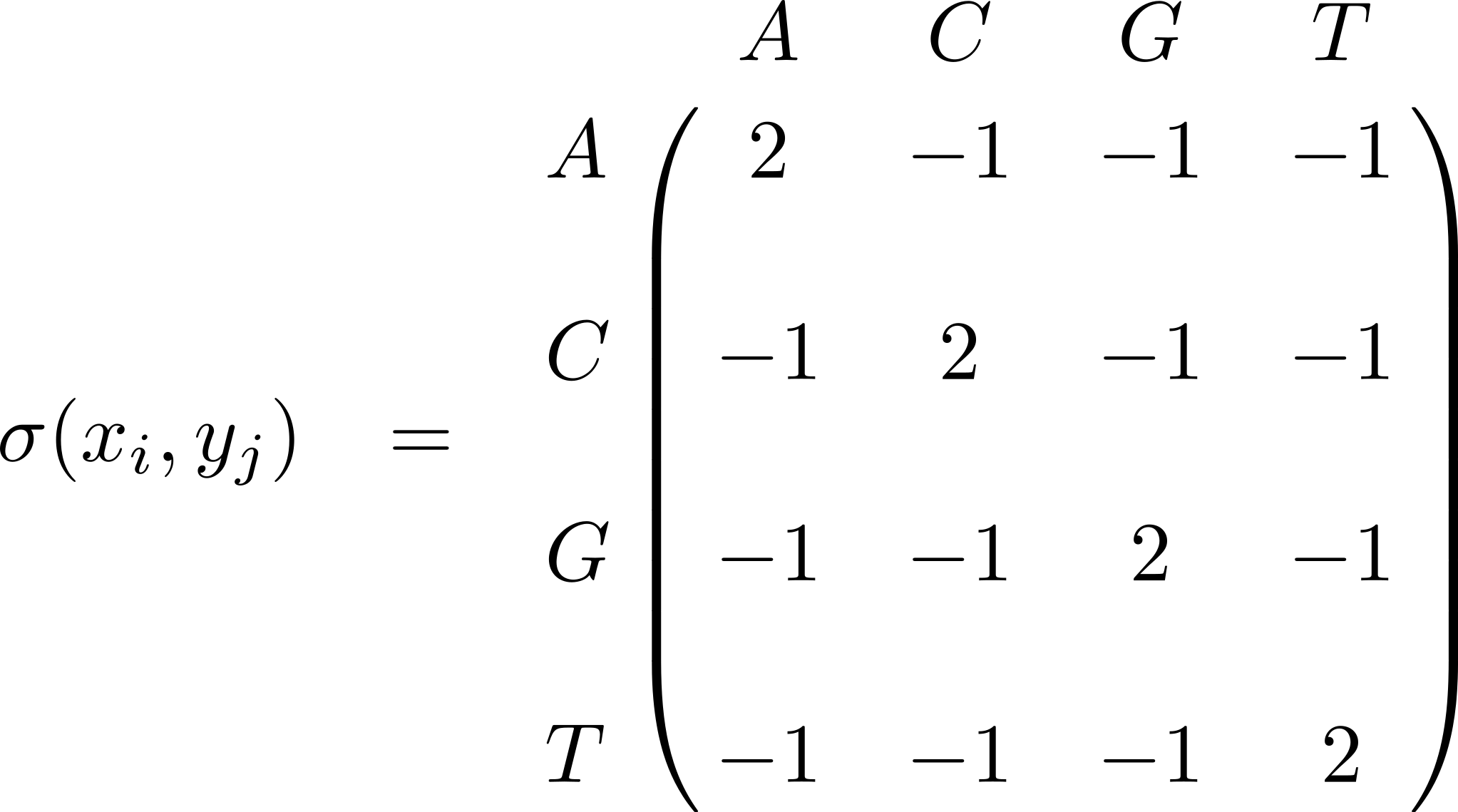
Exercise 1
1a)
Compute the Boltzmann-weighted score for the following alignments:
(a) x: --AGCGG (b) x: AGCGG------
||:|| :
y: ACAGGGG y: ----ACAGGGGHide
Hint 1 : Formulae
\[ S(a) = \sum_{x_i \sim y_j \in a} \sigma(x_i,y_j) + \sum \text{gap penalties}\\ e^{\frac{S(a)}{T}} = \Bigg(\prod_{x_i\sim y_j \in a} e^{\frac{\sigma(x_i,y_j)}{T}} \Bigg) \times e^{\frac{\sum \text{gap penalties}}{T}}\\ \]
Hint 2
For each alignment you only need to calculate \(e^x\) once.
Hint 3: Calculations
\[\begin{align*} \text{(a)} &\qquad e^{\sigma(A,A)} \times e^{3\sigma(G,G)} \times e^{\sigma(C,G)} \times e^{g(2)} &&= e^2 \times e^6 \times e^{-1} \times e^{-0.5 +(-0.25\times 2)} = e^6 \\ \text{(b)} &\qquad e^{\sigma(G,A)} \times e^{g(4)} \times e^{g(6)} &&= e^{-1} \times e^{0.5 + (-0.25\times 4)} \times e^{0.5 + (-0.25\times 6)} = e^{-4.5} \end{align*}\]
Solution
\[\begin{align*} \text{(a)} &\qquad e^6 = 403.43\\ \text{(b)} &\qquad e^{-4.5} = 0.011 \end{align*}\]
Exercise 2
2a)
Derive the recursion formula for \(Z^{I}_{i,j}\). Allow insertions after deletions and vice versa.
Hide
Solution
\[ Z^{I}_{i,j} = Z^{I}_{i,j-1} \times e^\frac{\beta}{T} + Z^{M}_{i,j-1} \times e^\frac{g(1)}{T} + Z^{D}_{i,j-1} \times e^\frac{g(1)}{T} \]
2b)
Compute the partition function Z(T) by dynamic programming for the
sequences x=ACC and y=AC. Allow insertions
after deletions and vice versa. In order to simplify the computations,
you can round to two digits after the decimal point. Please be aware
that we used exact numbers for all calculations and rounded in the
end.
Hide
Hint 1: Formulae
Initialization: \[\begin{align*} Z^M_{i,0} &= Z^M_{0,j} = 0, Z^M_{0,0} = 1\\ Z^I_{i,0} &= 0\\ Z^D_{0,j} &= 0 \end{align*}\]
Recursion: \[\begin{align*} Z^{M}_{i,j} &= Z_{i-1,j-1} \times e^{\frac{\sigma(x_i,y_j)}{T}}\\ Z^{I}_{i,j} &= Z^{I}_{i,j-1} \times e^\frac{\beta}{T} + Z^{M}_{i,j-1} \times e^\frac{g(1)}{T} + Z^{D}_{i,j-1} \times e^\frac{g(1)}{T}\\ Z^{D}_{i,j} &= Z^{D}_{i-1,j} \times e^\frac{\beta}{T} + Z^{M}_{i-1,j} \times e^\frac{g(1)}{T} + Z^{I}_{i-1,j} \times e^\frac{g(1)}{T}\\ Z_{i,j} &= Z^{M}_{i,j} + Z^{I}_{i,j} + Z^{D}_{i,j} \end{align*}\]
Solution
ZM | - | A | C |
|---|---|---|---|
- | 1 | 0.00 | 0.00 |
A | 0 | 7.39 | 0.17 |
C | 0 | 0.17 | 57.90 |
C | 0 | 0.14 | 30.42 |
ZI | - | A | C |
|---|---|---|---|
- | 0 | 0.47 | 0.37 |
A | 0 | 0.22 | 3.77 |
C | 0 | 0.17 | 2.00 |
C | 0 | 0.14 | 1.63 |
ZD | - | A | C |
|---|---|---|---|
- | 0.00 | 0.00 | 0.00 |
A | 0.47 | 0.22 | 0.17 |
C | 0.37 | 3.68 | 2.00 |
C | 0.29 | 3.10 | 29.85 |
Z | - | A | C |
|---|---|---|---|
- | 1.00 | 0.47 | 0.37 |
A | 0.47 | 7.84 | 4.12 |
C | 0.37 | 4.12 | 61.89 |
C | 0.29 | 3.37 | 61.90 |
Exercise 3
The partition function of the reverse sequences \(x^* = CCA\) and \(y^* = CA\) is given in the matrix \(Z^*\):
Z* | - | C | A |
|---|---|---|---|
- | 1.00 | 0.47 | 0.37 |
C | 0.47 | 7.84 | 4.12 |
C | 0.37 | 7.43 | 8.45 |
A | 0.29 | 4.94 | 61.90 |
3a)
Find a mapping from matrix \(Z^{*}_{k,l}\) to \(Z^{\prime}_{i,j}\). Which position in matrix \(Z^{*}\) corresponds to which position in matrix \(Z^{\prime}\)?
Hide
Solution
\(Z^{\prime}_{i,j}\) is the partition function of the alignment \(x_i ... x_{|x|}\) with \(y_j ... y_{|y|}\).
\(Z^{*}_{k,l}\) is the partition function of the alignment \(x_{|x|} ... x_{|x|-k+1}\) with \(y_{|y|}...y_{|y|-l+1}\).
\[\begin{align*} i &= |x| -k +1 \Leftrightarrow k = |x| -i +1\\ j &= |y| -l +1 \Leftrightarrow l = |y| -j +1 \end{align*}\]
Z* | - | C | A |
|---|---|---|---|
- | (0,0) | (0,1) | (0,2) |
C | (1,0) | (1,1) | (1,2) |
C | (2,0) | (2,1) | (2,2) |
A | (3,0) | (3,1) | (3,2) |
Z' | - | A | C | - |
|---|---|---|---|---|
- | (0,0) | (0,1) | (0,2) | (0,3) |
A | (1,0) | (1,1) | (1,2) | (1,3) |
C | (2,0) | (2,1) | (2,2) | (2,3) |
C | (3,0) | (3,1) | (3,2) | (3,3) |
- | (4,0) | (4,1) | (4,2) | (4,3) |
3b)
Use \(Z,Z^*\) and the mapping from \(Z^*\) to \(Z^\prime\) to compute the probability of the alignment edges \((1,1)\), \((2,2)\), \((3,1)\) and \((3,2)\) between \(x\) and \(y\).
Hide
Hint 1: Formulae
\[ P(x_i \sim y_j | x,y) = \frac{Z_{i-1,j-1}\times e^{\frac{\sigma(x_i,y_j)}{T}} \times Z^{\prime}_{i+1,j+1}}{Z(T)}\\ Z^M_{i,j} = Z_{i-1,j-1} \times e^{\frac{\sigma(x_i,y_j)}{T}} \]
Hint 2
Mapped positions: \[\begin{align*} Z^{\prime}_{2,2} &\Longleftrightarrow Z^{\ast}_{2,1}\\ Z^{\prime}_{3,3} &\Longleftrightarrow Z^{\ast}_{1,0}\\ Z^{\prime}_{4,2} &\Longleftrightarrow Z^{\ast}_{0,1}\\ Z^{\prime}_{4,3} &\Longleftrightarrow Z^{\ast}_{0,0} \end{align*}\]
Solution
Alignment edge \((1,1)\): \[ P(x_1 \sim y_1 | x,y) = \frac{Z_{0,0}\times e^{\frac{\sigma(x_1,y_1)}{T}} \times Z^{\prime}_{2,2}}{Z(T)} =\frac{Z_{0,0}\times e^{\frac{\sigma(x_1,y_1)}{T}} \times Z^{\ast}_{2,1}}{Z(T)} = \frac{Z^M_{1,1} \times Z^{\ast}_{2,1}}{Z(T)} = \frac{7.39 \times 7.43}{61.90} = 0.89 \] Alignment edge \((2,2)\): \[ P(x_2 \sim y_2 | x,y) = \frac{Z_{1,1}\times e^{\frac{\sigma(x_2,y_2)}{T}} \times Z^{\prime}_{3,3}}{Z(T)} =\frac{Z_{1,1}\times e^{\frac{\sigma(x_2,y_2)}{T}} \times Z^{\ast}_{1,0}}{Z(T)} = \frac{Z^M_{2,2} \times Z^{\ast}_{1,0}}{Z(T)} = \frac{57.90 \times 0.47}{61.90} = 0.44 \] Alignment edge \((3,1)\): \[ P(x_3 \sim y_1 | x,y) = \frac{Z^M_{3,1} \times Z^{\prime}_{4,2}}{Z(T)} = \frac{Z^M_{3,1} \times Z^{\ast}_{0,1}}{Z(T)} = \frac{0.14 \times 0.47}{61.90} = 0.001 \] Alignment edge \((3,2)\): \[ P(x_3 \sim y_2 | x,y) = \frac{Z^M_{3,2} \times Z^{\prime}_{4,3}}{Z(T)} = \frac{Z^M_{3,1} \times Z^{\ast}_{0,0}}{Z(T)} = \frac{30.42 \times 1}{61.90} = 0.49 \]