Exercise sheet 11: RNA Bioinformatics
Exercise 1
RNA secondary structures can be represented using a graph notation, where nodes represent nucleotides and edges encode the molecule’s backbone or intramolecular base pairs between nucleotides. Below, an RNA molecule graph is depicted that encodes base pairs in blue.
Decide for the following properties whether they are correct or wrong given the RNA secondary structure graph.
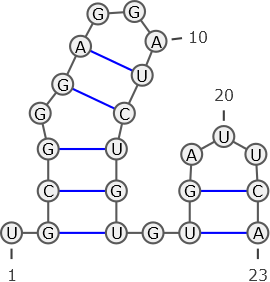
1a)
Position 23 represents the 5’-end
Hide
Solution
wrong; We always encode in the 5’ (=1) to 3’ (=n) direction.
1b)
the graph is invalid
Hide
Solution
wrong
1c)
contains invalid base pairs
Hide
Solution
wrong; all base pairs depicted in the graph are valid
1d)
contains a pseudoknot
Hide
Solution
wrong; There are no pseudoknot structures in this graph.
1e)
non-crossing
Hide
Solution
correct; There are no pseudoknot structures in this graph.
1f)
nested
Hide
Solution
correct
1g)
contains base pair (5,12)
Hide
Solution
wrong; Position 5 is unpaired.
1h)
contains base pair (4,13)
Hide
Solution
correct
1i)
base pair (1,10) would be crossing
Hide
Solution
correct
1j)
obeys a minimal loop length of 4
Hide
Solution
wrong; The minimum loop length for this graph is 3. (number of unpaired bases in loops)
1k)
encoded by ((…)).(((((…)).))).
Hide
Solution
wrong
1l)
encoded by .(((.((…))))).((…))
Hide
Solution
correct
Exercise 2
You are given the following dot-bracket string: (((…)))…((((…))..))
2a)
Draw graph representations of all nested structures that can be encoded by the dot-bracket string. Assume a minimal loop length of 3.
Hide
Solution
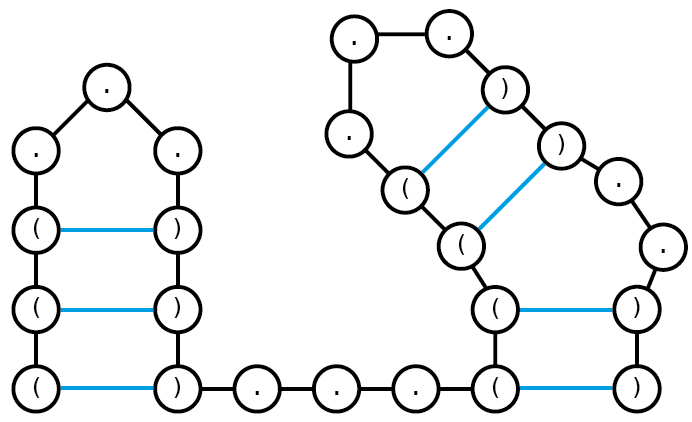
This is the only possible nested structure based on the dot-bracket string given.
2b)
Draw a graph representation of one possible crossing structure that can be encoded by the dot-bracket string. Assume a minimal loop length of 3.
Hide
Solution
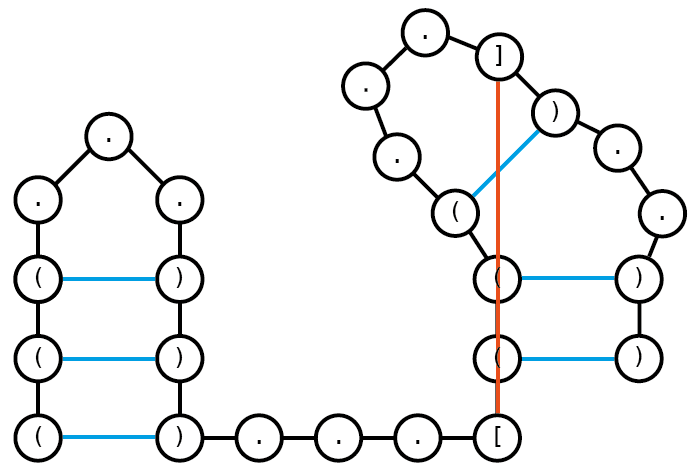
Dot-bracket string: (((…)))…[(((…])..))
There are multiple other possible crossing structures. (e.g. (((…)))…[((<…])..>) )
Exercise 3
Given the following partially filled Nussinov matrix \(N\) using a minimal loop length \(l = 0\), i.e. neighbored nucleotides are allowed to pair.
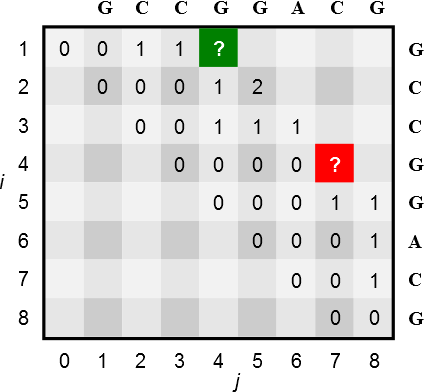
3a)
What are the values of the green and red entry?
Hide
Solution
green: \(2\)
red: \(1\)
3b)
How many tracebacks exist for the red entry using the original recursion by Nussinov?
Hide
Solution
There exist two tracebacks for the red entry; pairing with either G.
Exercise 4
Given any matrix \(N\) filled by Nussinov’s algorithm for and RNA sequence \(S\) of length \(n\). Discuss which of the following statements are correct or wrong.
The entry \(N_{1,n}\) of the Nussinov matrix encodes …
4a)
… the optimal structure.
Hide
Solution
wrong; It only encodes the base pair number for the optimal structure.
4b)
… the minimum free energy (mfe) structure.
Hide
Solution
wrong; No energy minimization is done.
4c)
… the maximal number of base pairs for sequence \(S_1\)..\(S_n\).
Hide
Solution
correct
4d)
… the traceback end.
Hide
Solution
wrong; It encodes the traceback start.
4e)
… the maximal number of base pairs for any structure.
Hide
Solution
correct
4f)
… information for a unique structure.
Hide
Solution
wrong; Typically there is more than one optimal structure with maximal number of base pairs.
Exercise 5
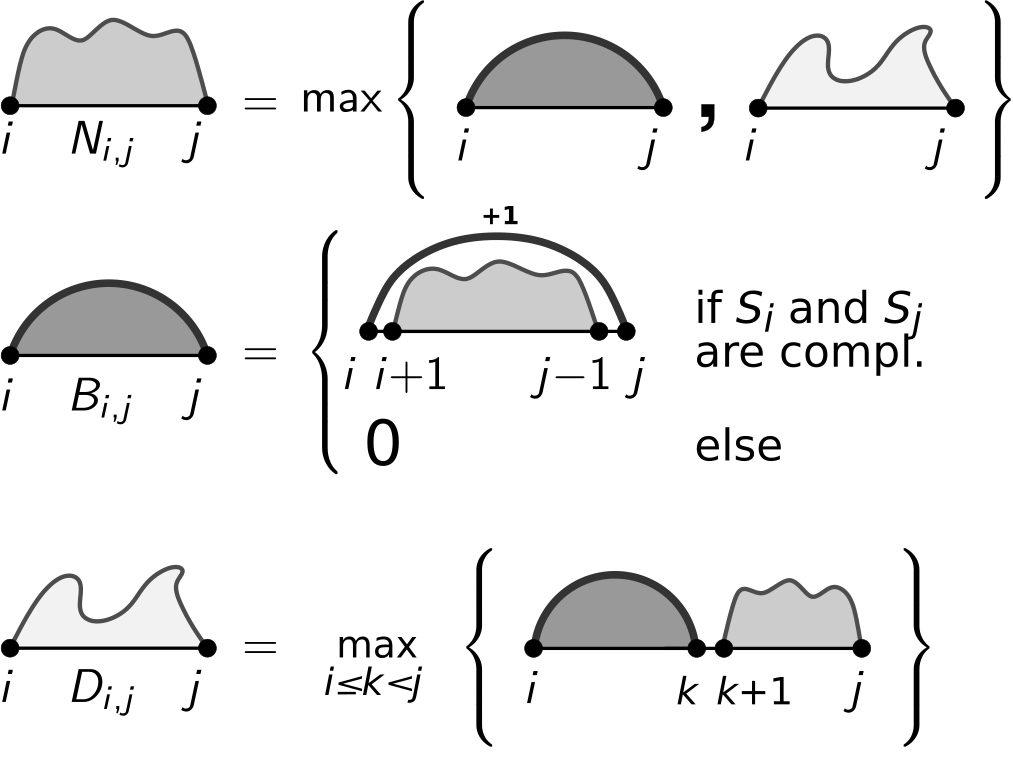
5a)
Provide all recursion and initialization details for the following recursion depictions. Note, also ensure a minimal loop length \(l\) within your recursions.
Hide
Solution
\[\begin{align*} N_{i,i} = N_{i,i-1} &=& 0 \text{ (no init for $B$ and $D$ needed)} \\ \forall_{1\leq i<j\leq n}: N_{i,j} &=& max\left\{ B_{i,j}, D_{i,j} \right\} \\ B_{i,j} &=& \begin{cases} N_{i+1,j-1}+1 & \text{ if }i+l<j \wedge S_i,S_j\text{ compl.}\\ 0 & \text{ else} \end{cases} \\ D_{i,j} &=& \max_{i\leq k<j} \left\{ B_{i,k} + N_{k+1,j} \right\} \text{ (only valid for $i<j$)} \end{align*}\]