Exercise sheet 7: BLAT
In the first step of the BLAT (Blast-like Alignment Tool) algorithm, regions that are likely to be homologous are detected. In this exercise sheet, we will investigate the search stage of the BLAT algorithm on the example of the mouse genome.
We want to determine whether a region from the human genome aligns to a part of the mouse genome. Therefore, a homologous region to our query sequence will be detected during the search stage.
We assume that:
- the human genome \(G\) is approximately \(2.9\) billion bases long.
- the mouse genome \(G\) is approximately \(2.5\) billion bases long.
- the match ratio \(M\) between homologous areas of both species is \(98\%\) for DNA and \(89\%\) for protein alignments.
- in our example we assume that homologous areas \(H\) are typically \(50\) bases long.
- our query sequence \(Q\) is GTCCTCGGAACCAGGACCTCGGCGTGGCCTAGCG.
In the following exercises, we will focus on the DNA sequences.
Exercise 1
For the \(K\)-mer sizes \(K=7\) and \(K=14\), respectively.
1a)
What is the probability of having a perfect match between a specific \(K\)-mer in a homologous region and a \(K\)-mer in the query sequence?
Hide
Formula
\[ p_{1} = M^K \]
Solution
For \(K=7\): \[ p_{1} = 0.98^{7} = 0.8681 \] For \(K=14\): \[ p_{1} = 0.98^{14} = 0.7536 \]
1b)
What is the probability that at least one non-overlapping \(K\)-mer in the homologous region matches perfectly with the corresponding \(K\)-mer in the query sequence?
Hide
Formula
\[ P = 1 - (1 - p_{1})^{T} = 1 - (1 - M^{K})^{T},\\ \text{with}\quad T= \left\lfloor\frac{H}{K}\right\rfloor \]
Solution
For \(K=7\): \[ P = 1 - (1 - 0.98^7)^{\left\lfloor\frac{50}{7}\right\rfloor} = 0.9999... \] For \(K=14\): \[ P = 1 - (1 - 0.98^{14})^{\left\lfloor\frac{50}{14}\right\rfloor} = 0.9850... \]
1c)
Calculate the number of False Positives (FPs), i.e. the number of \(K\)-mers that are expected to match by chance.
Hide
Formula
\[\begin{align*} F &= (Q-K+1) \times \bigg(\frac{G}{K}\bigg) \times \bigg(\frac{1}{A}\bigg)^{K},\\ &A: \text{the alphabet size}\\ &Q: \text{the query length in bases}\\ &G: \text{the genome size in bases} \end{align*}\]
Warning
This only holds under the assumption that all letters in the alphabet are equally likely!
Solution
For \(K=7\): \[ F = (34-7+1) \times \frac{2500000000}{7} \times \frac{1}{4}^{7} = 610351.5625 \] For \(K=14\): \[ F = (34-14+1) \times \frac{2500000000}{14} \times \frac{1}{4}^{14} = 13.9698 \]
1d)
Observe the True positive rate (TPR) and the number of False Positives for the \(7\)-mers and \(14\)-mers that you computed in part 1B and 1C. What observation do you make?
Hide
Solution
When increasing the \(K\)-mer size both the TPR and the number of False Positives are reduced. But the number of False Positives reduces drastically, compared to the TPR.
Exercise 2
In order to increase the True Positive Rate, we want to allow single mismatches when checking for exact matches.
For the \(K\)-mer sizes \(K=7\) and \(K=14\), respectively.
2a)
What is the probability that at least one non-overlapping \(K\)-mer in the homologous region matches perfectly with the corresponding \(K\)-mer in the query sequence? Given that we allow one mismatch.
Hide
Formula
\[ P = 1 - (1 - (M^{K}+K\times M^{K-1}\times (1-M)))^{T},\\ \text{with}\quad T= \left\lfloor\frac{H}{K}\right\rfloor \]
Solution
For \(K=7\): \[ P = 1 - (1 - (0.98^{7} + 7*0.98^{6}*0.02))^{\left\lfloor\frac{50}{7}\right\rfloor} \approx 1 \] For \(K=14\): \[ P = 1 - (1 - (0.98^{14} + 14*0.98^{13}*0.02))^{\left\lfloor\frac{50}{14}\right\rfloor} \approx 1 \]
2b)
Calculate the number of False Positives (FPs), i.e. the number of \(K\)-mers that are expected to match by chance. Given that we allow one mismatch.
Hide
Formula
\[\begin{align*} F &= (Q-K+1) \times \bigg(\frac{G}{K}\bigg) \times \Bigg[\bigg(\frac{1}{A}\bigg)^{K} + K \times \bigg(\frac{1}{A}\bigg)^{K-1} \times \bigg(1-\frac{1}{A}\bigg)\Bigg],\\ &A: \text{the alphabet size}\\ &Q: \text{the query length in bases}\\ &G: \text{the genome size in bases} \end{align*}\]
Solution
For \(K=7\): \[ F = (34-7+1) \times \frac{2500000000}{7} \times (\frac{1}{4}^{7} + 7 \times \frac{1}{4}^6 \times (1-\frac{1}{4})) = 1.3427... * 10^{7} \] For \(K=14\): \[ F = (34-14+1) \times \frac{2500000000}{14} \times (\frac{1}{4}^{14} + 14 \times \frac{1}{4}^{13} \times (1-\frac{1}{4})) = 600.7031 \]
2c)
What development do we see when observing the TPR and FPs for the updated formulae?
Hide
Solution
We observe an increase in both the TPR and the number of False positives.
Exercise 3
Finally, we want to reduce the number of False Positive results. To that end, instead of requiring single perfect matches, we now want at least \(n\) perfect matches.
For the \(K\)-mer sizes \(K=7\) and \(K=14\), respectively.
3a)
What is the probability that at least \(2\) non-overlapping \(K\)-mer in the homologous region match perfectly with corresponding \(K\)-mers in the query sequence?
Hide
Formula
\[ P_{n} = (M^{K})^{n} \times (1-M^{K})^{T-n} \times \frac{T!}{n! \times (T-n)!}\\ \text{with}\quad T= \left\lfloor\frac{H}{K}\right\rfloor\\\\ P = P_{n} + P_{n+1} + ... + P_{T} \]
Solution
For \(K=7\): \[ P_{2} = 0.98^{7 \times 2} \times (1-0.98^{7})^{\left\lfloor\frac{50}{7}\right\rfloor-2} \times \frac{\frac{50}{7}\text{!}}{2\text{!}\times(\frac{50}{7}-2)\text{!}}\\ \text{...}\\ \text{...}\\ \] \[\begin{align*} P &= P_{2} + P_{3} + P_{4} + P_{5} + P_{6} + P_{7}\\ &= 0.000631 + 0.006925 + 0.045591 + 0.180074 + 0.395142 + 0.371601\\ &= 0.999967... \end{align*}\]
For \(K=14\): \[ P_{2} = 0.98^{14 \times 2} \times (1-0.98^{14})^{\left\lfloor\frac{50}{14}\right\rfloor-2} \times \frac{\frac{50}{14}!}{2!\times(\frac{50}{14}-2)!}\\ \text{...}\\ \text{...}\\ \] \[\begin{align*} P &= P_{2} + P_{3}\\ &= 0.419776 + 0.428050\\ &= 0.847827... \end{align*}\]
3b)
We can observe a decrease in the TPR. Does it still make sense to use this method? Why?
Hide
Hint
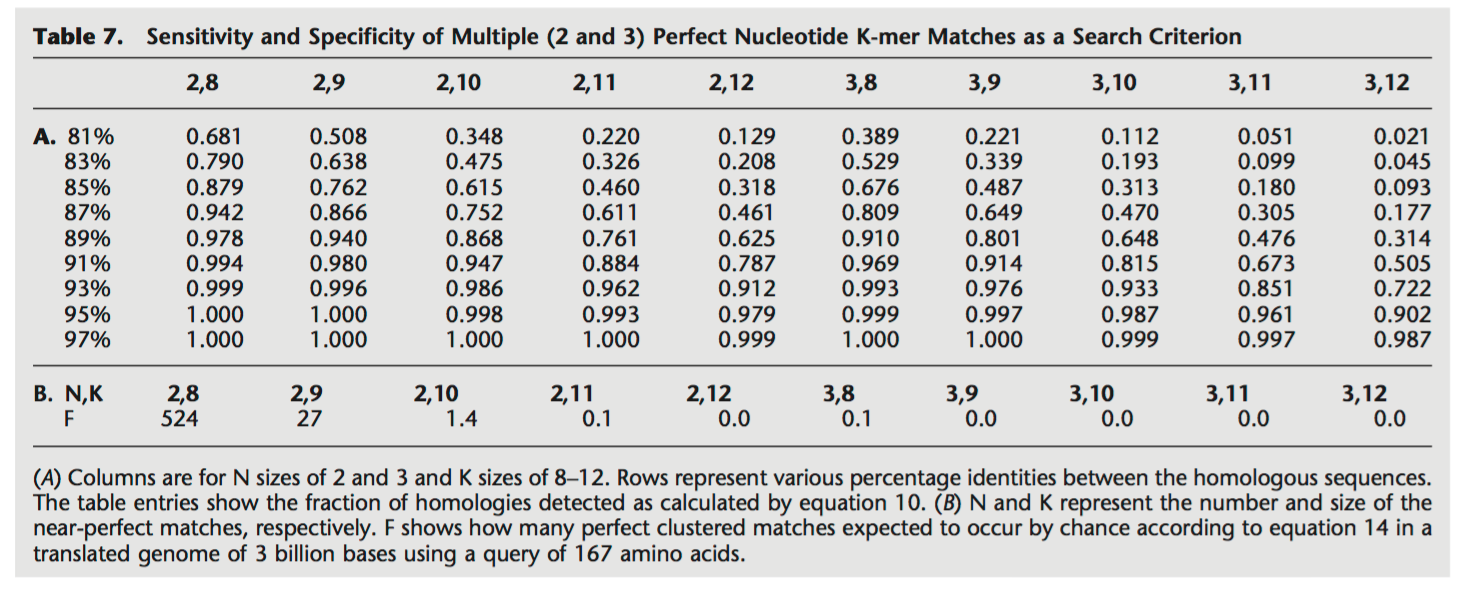
Solution
While it is true that this also decreases the TPR. It drastically decreases the amount of False Positives, which greatly improves the overall results. In real examples, the size of the homologous regions is typically higher than 50 nucleotides that we chose for this example. When considering our example with \(H=100\), we would end up with a TPR close to 1.0, while having nearly no False Positives.