Exercise sheet 2: Hidden Markov models II
Exercise 1 - The occasionally cheating casino
In a casino they use a fair die most of the time, but occasionally they switch to a loaded die. The loaded die has a probability \(0.5\) to show number six and probability \(0.1\) for the numbers one to five. Assume that the casino switches from a fair to a loaded die with probability \(0.05\) before each roll, and that the probability of switching back is \(0.1\). The probability to start a game with the fair die is \(0.9\).
1a)
Find the probability \(P(\mathcal{O}|M)\) for \(\mathcal{O}=1662\) and the given HMM using the forward algorithm.
Hide
Hint 1 : Formulae
\[\begin{align*} \alpha_{1}(i) =& \pi_{i} \times b_{i,o_1}\\ \alpha_{t+1}(j) =& \sum_{i\in\{F,L\}}\alpha_{t}(i)\times a_{i,j}\times b_{j,o_{t+1}} \end{align*}\]
Hint 2 : Calculation Method
\[\begin{align*} \alpha_1(F) =& \pi_F \times b_{F,1} = 0.9 \times \frac{1}{6} = 0.15\\ \alpha_1(L) =& \pi_L \times b_{L,1} = 0.1 \times 0.1 = 0.01\\\\ \alpha_2(F) =& \alpha_{1}(F)\times a_{F,F}\times b_{F,6} + \alpha_{1}(L)\times a_{L,F}\times b_{F,6} = 0.15 \times 0.95 \times \frac{1}{6} + 0.01 \times 0.1 \times \frac{1}{6} = 0.0239167\\ \alpha_2(L) =& \alpha_{1}(F)\times a_{F,L}\times b_{L,6} + \alpha_{1}(L)\times a_{L,L}\times b_{L,6} = 0.15 \times 0.05 \times 0.5 + 0.01 \times 0.9 \times 0.5 = 0.00825\\ \alpha_3(F) =& 0.023917 \times 0.95 \times \frac{1}{6} + 0.00825 \times 0.1 \times \frac{1}{6} = 0.00392\\ \alpha_3(L) =& 0.023917 \times 0.05 \times 0.5 + 0.00825 \times 0.9 \times 0.5 = 0.00431\\ \alpha_4(F) =& 0.00392 \times 0.95 \times \frac{1}{6} + 0.00431 \times 0.1 \times \frac{1}{6} = 0.000693\\ \alpha_4(L) =& 0.00392 \times 0.05 \times 0.1 + 0.00431 \times 0.9 \times 0.1 = 0.000407\\ \end{align*}\]
Solution
\[ P( \mathcal{O}=1662)= \alpha_4(F)+\alpha_4(L) = 0.000693 + 0.000407 = 0.0011 \]
1b)
Given the result of Question 1A, do you expect a higher probability for the observations \(\mathcal{O} = 1666\) and \(\mathcal{O} = 1262\)?
Hide
Hint 1
It has something to do with the emission probabilities of the different states.
Solution
As state L has a high probability to emit a six, observations with more sixes are more likely.
\[ P(\mathcal{O} = 1666) > P(\mathcal{O} = 1662) > P(\mathcal{O} = 1262) \]
1c)
Find the most probable path through the HMM that produces the sequence \(\mathcal{O} = 1662\).
Hide
Hint 1 : Formulae
\[\begin{align*} \delta_{1}(i) =& \pi_{i} \times b_{i,o_1}\\ \delta_{t+1}(j) =& max_{i\in\{F,L\}}\delta_{t}(i)\times a_{i,j} \times b_{j,o_{t+1}}\\ q_{t}^{ * } =& argmax_{1 \leq i \leq n} \{ \delta_t(i) a_{i,q_{t+1}^{ * } } \} \end{align*}\]
Hint 2 : Intermediate calculations
\[\begin{align*} \delta_1(F) =& \pi_F \times b_{F,1} = 0.9 \times \frac{1}{6} = 0.15\\ \delta_1(L) =& \pi_F \times b_{L,1} = 0.1 \times 0.1 = 0.01\\\\ \delta_2(F) =& max(\delta_{1}(F) \times a_{F,F} \times b_{F,6}, \delta_{1}(L) \times a_{L,F} \times b_{F,6}) = max(0.02375 , 0.00016) = 0.02375 \\ \delta_2(L) =& max(\delta_{1}(F) \times a_{F,L} \times b_{L,6}, \delta_{1}(L) \times a_{L,L} \times b_{L,6}) = max(0.00375, 0.0045) = 0.0045\\ \delta_3(F) =& max(0.00376, 0.000075) = 0.00376\\ \delta_3(L) =& max(0.00059375, 0.002025) = 0.002025\\ \delta_4(F) =& max(0.0005953, 0.00003375) = 0.0005953\\ \delta_4(L) =& max(0.0000188, 0.00018225) = 0.00018225\\\\ P( \mathcal{P}^{*}, \mathcal{O}) =& max(\delta_4(F), \delta_4(L)) = 5.95 \times 10^{-4} \end{align*}\]
Solution
\[\begin{align*} q_4^* =& argmax_{i\in\{F,L\}}(\delta_4(i)) = F\\ q_3^* =& argmax_{i\in\{F,L\}}(\delta_3(i) \times a_{i,q_4^*}) = argmax(F:0.00376 \times 0.95, L:0.002025 \times 0.1) = F\\ q_2^* =& argmax_{i\in\{F,L\}}(\delta_2(i) \times a_{i,q_3^*}) = argmax(F:0.02375 \times 0.95, L:0.0045 \times 0.1) = F\\ q_1^* =& argmax_{i\in\{F,L\}}(\delta_1(i) \times a_{i,q_2^*}) = argmax(F:0.15 \times 0.95, L:0.01 \times 0.1) = F\\ \Rightarrow& Q^*=FFFF \end{align*}\]
The best path is therefore to stay in state F.
Exercise 2 - Profile HMMs
Profile HMMs define a position specific scoring scheme which can be used to search databases for homologous sequences.
The following multiple alignment of DNA sequences is given:
AC---A
A----A
AG---T
TTGGGT
** *2a)
Draw the graphical representation of the profile HMM for the given multiple alignment.
Hide
Solution 1
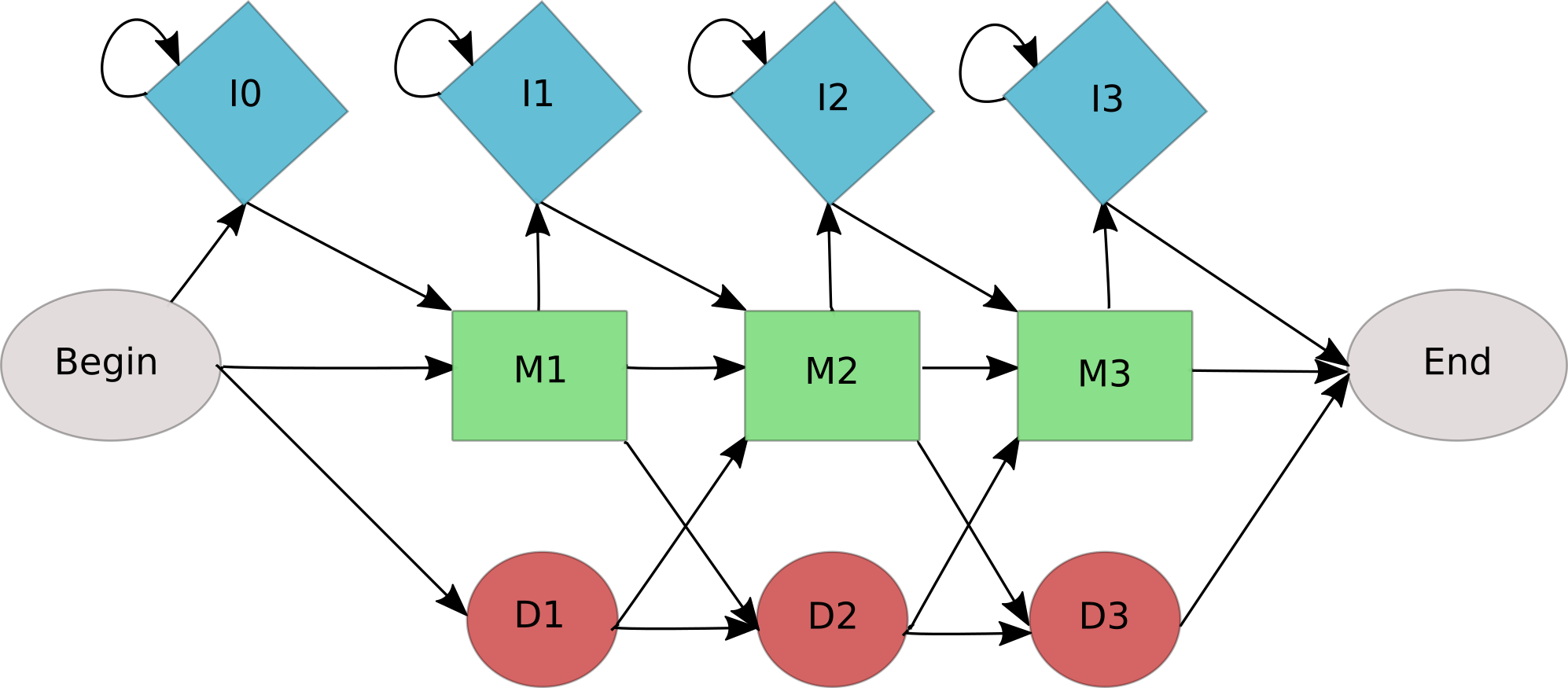
Solution 2
Since some of the transition probabilities will be zero (dotted lines) we can remove corresponding states (transparent).
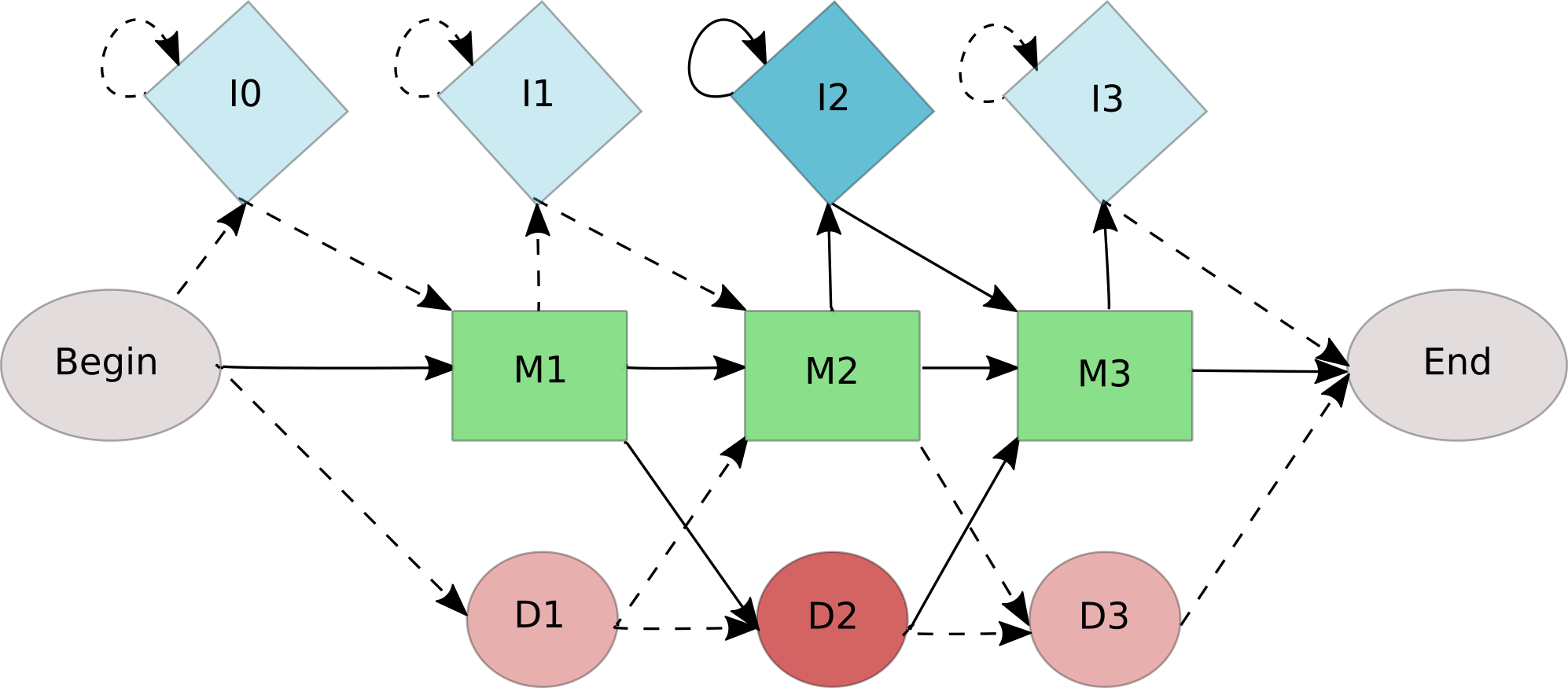
2b)
Find the state sequences that correspond to each row in the alignment.
Hide
Solution
AC---A M1 M2 M3
A----A M1 D2 M3
AG---T M1 M2 M3
TTGGGT M1 M2 I2 I2 I2 M32c)
Compute the following emission probabilities with maximum likelihood estimation: \(b_{M_1,A}\), \(b_{M_1,G}\), \(b_{M_1,C}\), \(b_{M_1,T}\).
Hide
Formulae
\[ b_{i,k} = \frac{E[\text{number of emissions of } \sigma_k \text{, while in state } i | \mathcal{O}, M]}{E[\text{number of times in state } i | \mathcal{O}, M]} \]
Solution
\(b_{M_1,A}=\frac{3}{4}\)
\(b_{M_1,G}=0\)
\(b_{M_1,C}=0\)
\(b_{M_1,T}=\frac{1}{4}\)
2d)
Compute the following transition probabilities with maximum likelihood estimation: \(a_{M_2,M_3}\), \(a_{M_2,I_2}\), \(a_{M_2,D_3}\)
Hide
Formulae
\[ a_{i,j} = \frac{E[\text{number of transitions from } i \text{ to } j | \mathcal{O}, M]}{E[\text{number of transitions from } i | \mathcal{O}, M]} \]
Solution
\(a_{M_2,M_3} = \frac{2}{2+1+0} = \frac{2}{3}\)
\(a_{M_2,I_2} = \frac{1}{2+1+0} = \frac{1}{3}\)
\(a_{M_2,D_3} = \frac{0}{2+1+0} = 0\)
2e)
Repeat the calculations from c) and d) using a pseudo-count of \(1\).
Hide
Solution
\(b_{M_1,A}=\frac{3+1}{4+4}=\frac{1}{2}\)
\(b_{M_1,G}=\frac{0+1}{4+4}=\frac{1}{8}\)
\(b_{M_1,C}=\frac{0+1}{4+4}=\frac{1}{8}\)
\(b_{M_1,T}=\frac{1+1}{4+4}=\frac{1}{4}\)
\(a_{M_2,M_3} = \frac{2+1}{2+1+0+3} = \frac{1}{2}\)
\(a_{M_2,I_2} = \frac{1+1}{2+1+0+3} = \frac{1}{3}\)
\(a_{M_2,D_3} = \frac{0+1}{2+1+0+3} = \frac{1}{6}\)